Advertisements
Online Mock Tests
Chapters
2: Numbers and Sequences
3: Algebra
4: Geometry
5: Coordinate Geometry
6: Trigonometry
7: Mensuration
8: Statistics and Probability
![Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 1 - Relations and Functions Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 1 - Relations and Functions - Shaalaa.com](/images/mathematics-english-class-10-sslc-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 1: Relations and Functions
Below listed, you can find solutions for Chapter 1 of Tamil Nadu Board of Secondary Education Samacheer Kalvi for Mathematics [English] Class 10 SSLC TN Board.
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 1 Relations and Functions Exercise 1.1 [Page 6]
Find A × B, A × A and B × A :
A = {2, −2, 3} and B = {1, −4}
Find A × B, A × A and B × A :
A = B = {p, q}
Find A × B, A × A and B × A:
A = {m, n}; B = Φ
Let A = {1, 2, 3} and B = {x | x is a prime number less than 10}. Find A × B and B × A
If B × A = {(-2, 3), (-2, 4), (0, 3), (0, 4), (3, 3), (3, 4)} find A and B
If A = {5, 6}, B = {4, 5, 6}, C = {5, 6, 7}, Show that A × A = (B × B) ∩ (C × C)
Given A = {1, 2, 3}, B = {2, 3, 5}, C = {3, 4} and D = {1, 3, 5}, check if (A ∩ C) × (B ∩ D) = (A × B) ∩ (C × D) is true?
Let A = {x ∈ W | x < 2}, B = {x ∈ N | 1 < x < 4} and C = {3, 5}. Verify that A × (B ∪ C) = (A × B) ∪ (A × C)
Let A = {x ∈ W | x < 2}, B = {x ∈ N | 1 < x < 4} and C = {3, 5}. Verify that A × (B ∩ C) = (A × B) ∩ (A × C)
Let A = {x ∈ W | x < 2}, B = {x ∈ N | 1 < x < 4} and C = {3, 5}. Verify that (A ∪ B) × C = (A × C) ∪ (B × C)
Let A = The set of all natural number less than 8, B = The set of all prime numbers less than 8, C = The set of even prime number. Verify that (A ∩ B) × C = (A × C) ∩ (B × C)
Let A = The set of all natural number less than 8, B = The set of all prime numbers less than 8, C = The set of even prime number. Verify that A × (B – C) = (A × B) – (A × C)
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 1 Relations and Functions Exercise 1.2 [Page 9]
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R1 = {(2, 1), (7, 1)}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R2 = {(–1, 1)}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R3 = {(2, –1), (7, 7), (1, 3)}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R4 = {(7, –1), (0, 3), (3, 3), (0, 7)}
Let A = {1, 2, 3, 4, …, 45} and R be the relation defined as “is square of ” on A. Write R as a subset of A × A. Also, find the domain and range of R
A Relation R is given by the set `{(x, y)/y = x + 3, x ∈ {0, 1, 2, 3, 4, 5}}`. Determine its domain and range
Represent the given relation by
(a) an arrow diagram
(b) a graph and
(c) a set in roster form, wherever possible
{(x, y) | x = 2y, x ∈ {2, 3, 4, 5}, y ∈ {1, 2, 3, 4}
Represent the given relation by
(a) an arrow diagram
(b) a graph and
(c) a set in roster form, wherever possible
{(x, y) | y = x + 3, x, y are natural numbers < 10}
A company has four categories of employees given by Assistants (A), Clerks (C), Managers (M), and an Executive Officer (E). The company provides ₹ 10,000, ₹ 25,000, ₹ 50,000, and ₹ 1,00,000 as salaries to the people who work in the categories A, C, M, and E respectively. If A1, A2, A3, A4, and A5 were Assistants; C1, C2, C3, C4 were Clerks; M1, M2, M3 were managers and E1, E2 was Executive officers and if the relation R is defined by xRy, where x is the salary given to person y, express the relation R through an ordered pair and an arrow diagram
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 1 Relations and Functions Exercise 1.3 [Pages 13 - 15]
Let f = {(x, y) | x, y ∈ N and y = 2x} be a relation on N. Find the domain, co-domain and range. Is this relation a function?
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
Given the function f: x → x2 – 5x + 6, evaluate f(– 1)
Given the function f: x → x2 – 5x + 6, evaluate f(2a)
Given the function f: x → x2 – 5x + 6, evaluate f(2)
Given the function f: x → x2 – 5x + 6, evaluate f(x – 1)
A graph representing the function f(x) is given in it is clear that f(9) = 2
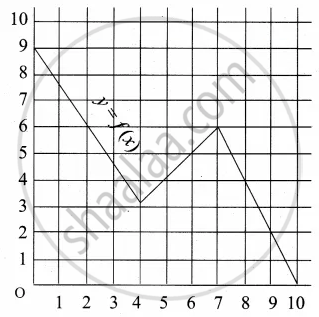
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
A graph representing the function f(x) is given in it is clear that f(9) = 2
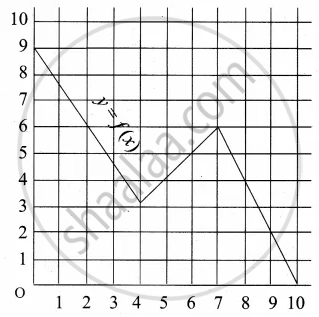
For what value of x is f(x) = 1?
A graph representing the function f(x) is given in it is clear that f(9) = 2
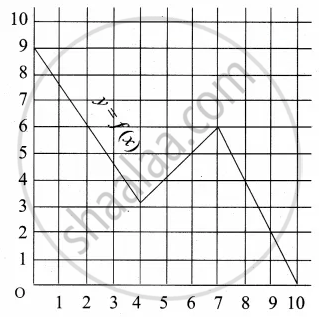
Describe the following Domain
A graph representing the function f(x) is given in it is clear that f(9) = 2
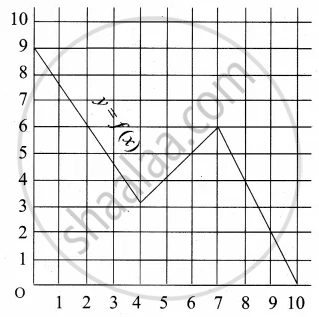
Describe the following Range
A graph representing the function f(x) is given in it is clear that f(9) = 2
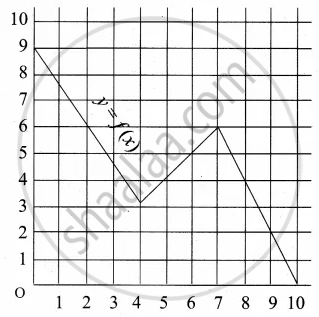
What is the image of 6 under f?
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
A function f is defined by f(x) = 2x – 3 find `("f"(0) + "f"(1))/2`
A function f is defined by f(x) = 2x – 3 find x such that f(x) = 0
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
A function f is defined by f(x) = 2x – 3 find x such that f(x) = f(1 – x)
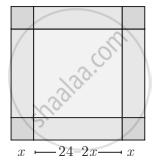
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Check if this relation is a function
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Find a and b
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Find the height of a person whose forehand length is 40 cm
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Find the length of forehand of a person if the height is 53.3 inches
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 1 Relations and Functions Exercise 1.4 [Pages 24 - 25]
Determine whether the graph given below represent function. Give reason for your answer concerning graph
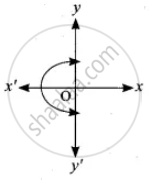
Determine whether the graph given below represent function. Give reason for your answer concerning graph
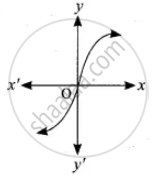
Determine whether the graph given below represent function. Give reason for your answer concerning graph
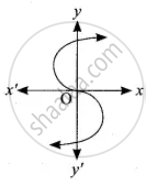
Determine whether the graph given below represent function. Give reason for your answer concerning graph
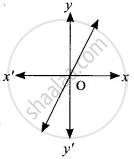
Let f: A → B be a function defined by f(x) = `x/2` – 1, where A = {2, 4, 6, 10, 12}, B = {0, 1, 2, 4, 5, 9}. Represent f by set of ordered pairs
Let f: A → B be a function defined by f(x) = `x/2` – 1, where A = {2, 4, 6, 10, 12}, B = {0, 1, 2, 4, 5, 9}. Represent f by a table
Let f: A → B be a function defined by f(x) = `x/2` – 1, where A = {2, 4, 6, 10, 12}, B = {0, 1, 2, 4, 5, 9}. Represent f by an arrow diagram
Let f: A → B be a function defined by f(x) = `x/2` – 1, where A = {2, 4, 6, 10, 12}, B = {0, 1, 2, 4, 5, 9}. Represent f by a graph
Represent the function f = {(1, 2), (2, 2), (3, 2), (4, 3), (5, 4)} through an arrow diagram
Represent the function f = {(1, 2), (2, 2), (3, 2), (4, 3), (5, 4)} through a table form
Represent the function f = {(1, 2), (2, 2), (3, 2), (4, 3), (5, 4)} through a graph
Show that the function f : N → N defined by f(x) = 2x – 1 is one-one but not onto
Show that the function f : N → N defined by f(m) = m2 + m + 3 is one-one function
Let A = {1, 2, 3, 4} and B = N. Let f : A → B be defined by f(x) = x3 then, find the range of f
Let A = {1, 2, 3, 4} and B = N. Let f : A → B be defined by f(x) = x3 then, identify the type of function
In the following case state whether the function is bijective or not. Justify your answer
f: R → R defined by f(x) = 2x + 1
In the following case state whether the function is bijective or not. Justify your answer
f: R → R defined by f(x) = 3 – 4x2
Let A = {–1, 1} and B = {0, 2}. If the function f: A → B defined by f(x) = ax + b is an onto function? Find a and b
If the function f is defined by f(x) = `{{:(x + 2";", x > 1),(2";", -1 ≤ x ≤ 1),(x - 1";", -3 < x < -1):}` find the value of f(3)
If the function f is defined by f(x) = `{{:(x + 2";", x > 1),(2";", -1 ≤ x ≤ 1),(x - 1";", -3 < x < -1):}` find the value of f(0)
If the function f is defined by f(x) = `{{:(x + 2";", x > 1),(2";", -1 ≤ x ≤ 1),(x - 1";", -3 < x < -1):}` find the value of f(− 1.5)
If the function f is defined by f(x) = `{{:(x + 2";", x > 1),(2";", -1 ≤ x ≤ 1),(x - 1";", -3 < x < -1):}` find the value of f(2) + f(– 2)
A function f: [– 5, 9] → R is defined as follow :
f(x) = `{{:(6x + 1";", -5 ≤ x < 2),(5x^2 - 1";", 2 ≤ x < 6),(3x - 4";", 6 ≤ x ≤ 9):}` Find f(– 3) + f(2)
A function f: [– 5, 9] → R is defined as follow :
f(x) = `{{:(6x + 1";", -5 ≤ x < 2),(5x^2 - 1";", 2 ≤ x < 6),(3x - 4";", 6 ≤ x ≤ 9):}` Find f(7) – f(1)
A function f: [– 5, 9] → R is defined as follow :
f(x) = `{{:(6x + 1";", -5 ≤ x < 2),(5x^2 - 1";", 2 ≤ x < 6),(3x - 4";", 6 ≤ x ≤ 9):}` Find 2f(4) + f(8)
A function f: [– 5, 9] → R is defined as follow :
f(x) = `{{:(6x + 1";", -5 ≤ x < 2),(5x^2 - 1";", 2 ≤ x < 6),(3x - 4";", 6 ≤ x ≤ 9):}` Find `(2"f"(- 2) - "f"(6))/("f"(4) + "f"( -2))`
The distance S object travel under the influence of gravity in time t seconds is given by S(t) = `1/2` gt2 + at + b where, (g is the acceleration due to gravity), a, b are constant. Verify whether the function S(t) is one-one or not.
The function ‘t’ which map temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C) = F where F = `9/5` C + 32. Find, t(0)
The function ‘t’ which map temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C) = F where F = `9/5` C + 32. Find, t(28)
The function ‘t’ which map temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C) = F where F = `9/5` C + 32. Find, t(– 10)
The function ‘t’ which map temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C) = F where F = `9/5` C + 32. Find, the value of C when t(C) = 212
The function ‘t’ which map temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C) = F where F = `9/5` C + 32. Find, the temperature when the Celsius value is equal to the Fahrenheit value
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 1 Relations and Functions Exercise 1.5 [Pages 31 - 32]
Using the function f and g given below, find fog and gof. Check whether fog = gof
f(x) = x – 6, g(x) = x2
Using the function f and g given below, find fog and gof. Check whether fog = gof
f(x) = `(2)/x`, g(x) = 2x2 – 1
Using the function f and g given below, find fog and gof. Check whether fog = gof
f(x) = `(x + 6)/3`, g(x) = 3 – x
Using the function f and g given below, find fog and gof. Check whether fog = gof
f(x) = 3 + x, g(x) = x – 4
Using the function f and g given below, find fog and gof. Check whether fog = gof
f(x) = 4x2 – 1, g(x) = 1 + x
Find the value of k, such that fog = gof
f(x) = 3x + 2, g(x) = 6x – k
Find the value of k, such that fog = gof
f(x) = 2x – k, g(x) = 4x + 5
If f(x) = 2x – 1, g(x) = `(x + 1)/(2)`, show that fog = gof = x
If f(x) = x2 – 1, g(x) = x – 2 find a, if gof(a) = 1
Find k, if f(k) = 2k – 1 and fof(k) = 5
Let A, B, C ⊆ N and a function f: A → B be defined by f(x) = 2x + 1 and g: B → C be defined by g(x) = x2. Find the range of fog and gof.
If f(x) = x2 – 1. Find fof
If f(x) = x2 – 1. Find fofof
If f : R → R and g : R → R are defined by f(x) = x5 and g(x) = x4 then check if f, g are one-one and fog is one-one?
Consider the function f(x), g(x), h(x) as given below. Show that (fog)oh = fo(goh)
f(x) = x – 1, g(x) = 3x + 1 and h(x) = x2
Consider the function f(x), g(x), h(x) as given below. Show that (fog)oh = fo(goh)
f(x) = x2, g(x) = 2x and h(x) = x + 4
Consider the function f(x), g(x), h(x) as given below. Show that (fog)oh = fo(goh)
f(x) = x – 4, g(x) = x2 and h(x) = 3x – 5
Let f = {(–1, 3), (0, –1), (2, –9)} be a linear function from Z into Z. Find f(x)
In electrical circuit theory, a circuit C(t) is called a linear circuit if it satisfies the superposition principle given by C(at1 + bt2) = aC(t1) + bC(t2), where a, b are constants. Show that the circuit C(t) = 3t is linear.
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 1 Relations and Functions Exercise 1.6 [Pages 32 - 33]
Multiple Choice Question :
If n(A × B) = 6 and A = {1, 3} then n(B) is ________
1
2
3
6
Multiple Choice Question :
A = {a, b, p}, B = {2, 3}, C = {p, q, r, s} then n[(A ∪ C) × B] is _______
8
20
12
16
Multiple Choice Question :
If A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8} then state which of the following statement is true ______
(A × C) ⊂ (B × D)
(B × D) ⊂ (A × C)
(A × B) ⊂ (A × D)
(D × A) ⊂ (B × A)
Multiple Choice Question :
If there are 1024 relation from a set A = {1, 2, 3, 4, 5} to a set B, then the number of elements in B is
3
2
4
8
Multiple Choice Question :
The range of the relation R = {(x, x2) | x is a prime number less than 13} is ________
{2, 3, 5, 7}
{2, 3, 5, 7, 11}
{4, 9, 25, 49, 121}
{1, 4, 9, 25, 49, 121}
Multiple Choice Question :
If the ordered pairs (a + 2, 4) and (5, 2a + b) are equal then (a, b) is
(2, – 2)
(5, 1)
(2, 3)
(3, – 2)
Multiple Choice Question :
Let n(A) = m and n(B) = n then the total number of non-empty relation that can be defined from A to B is ________.
mn
nm
2mn – 1
2mn
Multiple Choice Question :
If {(a, 8), (6, b)} represent an identity function, then the value of a and b are respectively
(8, 6)
(8, 8)
(6, 8)
(6, 6)
Multiple choice question :
Let A = {1, 2, 3, 4} and B = {4, 8, 9, 10}. A function f: A → B given by f = {(1, 4), (2, 8), (3, 9), (4, 10)} is a
Many-one function
Identity function
One-to-one function
Into function
Multiple choice question :
If f(x) = 2x2 and g(x) = `1/(3x)`, then fog is
`3/(2x^2)`
`3/(3x^2)`
`2/(9x^2)`
`1/(6x^2)`
Multiple choice question :
If f : A → B is a bijective function and if n(B) = 7, then n(A) is equal to
7
49
1
14
Multiple choice question :
Let f and g be two function given by f = {(0, 1), (2, 0), (3, – 4), (4, 2), (5, 7)} g = {(0, 2), (1, 0), (2, 4), (– 4, 2), (7, 0) then the range of fog is
{0, 2, 3, 4, 5}
{– 4, 1, 0, 2, 7}
{1, 2, 3, 4, 5}
{0, 1, 2}
Multiple choice question :
Let f(x) = `sqrt(1 + x^2)` then
f(xy) = f(x).f(y)
f(xy) ≥ f(x).f(y)
f(xy) ≤ f(x).f(y)
None of these
Multiple choice question :
If g = {(1, 1), (2, 3), (3, 5), (4, 7)} is a function given by g(x) = αx + β then the value of α and β are
(– 1, 2)
(2, – 1)
(– 1, – 2)
(1, 2)
Multiple choice question :
f(x) = (x + 1)3 – (x – 1)3 represent a function which is
linear
cubic
reciprocal
quadratic
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board 1 Relations and Functions Unit Exercise – 1 [Pages 33 - 34]
If the ordered pairs (x2 – 3x, y2 + 4y) and (– 2, 5) are equal, then find x and y
The Cartesian product A × A has 9 elements among which (– 1, 0) and (0, 1) are found. Find the set A and the remaining elements of A × A
Given that f(x) = `{{:(sqrt(x - 1), x ≥ 1),(4, x < 1):}` Find f(0)
Given that f(x) = `{{:(sqrt(x - 1), x ≥ 1),(4, x < 1):}` Find f(3)
Given that f(x) = `{{:(sqrt(x - 1), x ≥ 1),(4, x < 1):}` Find f(a + 1) in terms of a. (Given that a ≥ 0)
Let A = {9, 10, 11, 12, 13, 14, 15, 16, 17} and let f : A → N be defined by f(n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f
Find the domain of the function f(x) = `sqrt(1 + sqrt(1 - sqrt(1 - x^2)`
If f(x)= x2, g(x) = 3x and h(x) = x – 2 Prove that (fog)oh = fo(goh)
Let A = {1, 2} and B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify whether A × C is a subset of B × D?
If f(x) = `(x - 1)/(x + 1), x ≠ - 1` Show that f(f(x)) = `- 1/x`, Provided x ≠ 0
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Write an expression for gf(x) in its simplest form
Write the domain of the following real function:
f(x) = `(2x + 1)/(x - 9)`
Write the domain of the following real function:
p(x) = `(-5)/(4x^2 + 1)`
Write the domain of the following real function:
g(x) = `sqrt(x - 2)`
Write the domain of the following real function:
h(x) = x + 6
Solutions for 1: Relations and Functions
![Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 1 - Relations and Functions Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 1 - Relations and Functions - Shaalaa.com](/images/mathematics-english-class-10-sslc-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Samacheer Kalvi solutions for Mathematics [English] Class 10 SSLC TN Board chapter 1 - Relations and Functions
Shaalaa.com has the Tamil Nadu Board of Secondary Education Mathematics Mathematics [English] Class 10 SSLC TN Board Tamil Nadu Board of Secondary Education solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Samacheer Kalvi solutions for Mathematics Mathematics [English] Class 10 SSLC TN Board Tamil Nadu Board of Secondary Education 1 (Relations and Functions) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Samacheer Kalvi textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 10 SSLC TN Board chapter 1 Relations and Functions are Introduction of Relations and Functions, Ordered Pair, Cartesian Product, Composition of Functions, Representation of Functions, Types of Functions, Special Cases of Functions, Identifying the Graphs of Linear, Quadratic, Cubic and Reciprocal Functions, Concept of Functions, Concept of Relation.
Using Samacheer Kalvi Mathematics [English] Class 10 SSLC TN Board solutions Relations and Functions exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Samacheer Kalvi Solutions are essential questions that can be asked in the final exam. Maximum Tamil Nadu Board of Secondary Education Mathematics [English] Class 10 SSLC TN Board students prefer Samacheer Kalvi Textbook Solutions to score more in exams.
Get the free view of Chapter 1, Relations and Functions Mathematics [English] Class 10 SSLC TN Board additional questions for Mathematics Mathematics [English] Class 10 SSLC TN Board Tamil Nadu Board of Secondary Education, and you can use Shaalaa.com to keep it handy for your exam preparation.
