Advertisements
Advertisements
प्रश्न
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
उत्तर
`"gg" (1/2) = "g"["g"(1/2)]`
= `"g"[1/2 - 2 ÷ 3]`
= `"g"[(1 - 4)/2 ÷ 3]`
= `"g"[(-3)/2 xx 1/3]`
= `"g"[- 1/2]`
= `[- 1/2 - 2 ÷ 3]`
= `[(-1 - 4)/2 ÷ 3]`
= `[(-5)/2 xx 1/3]`
`"gg" (1/2) = - 5/6`
APPEARS IN
संबंधित प्रश्न
If \[f\left( x \right) = x^3 - \frac{1}{x^3}\] , show that
The range of f(x) = cos [x], for π/2 < x < π/2 is
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
lf f(x) = 3(4x+1), find f(– 3)
A graph representing the function f(x) is given in it is clear that f(9) = 2
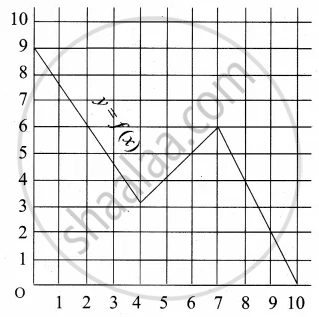
Describe the following Range
The domain of the function f(x) = log3+x (x2 - 1) is ______.
Let f : R → R be defined by
f(x) = `{(3x; x > 2),(2x^2; 1 ≤ x ≤ 2), (4x; x < 1):}`
Then f(-2) + f(1) + f(3) is ______
The domain of the function f given by f(x) = `(x^2 + 2x + 1)/(x^2 - x - 6)` is ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
