Advertisements
Advertisements
प्रश्न
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Check if this relation is a function
उत्तर
The relation is y = 0.9 x + 24.5
Yes, the relation is a function.
APPEARS IN
संबंधित प्रश्न
Write the range of the function f(x) = sin [x], where \[\frac{- \pi}{4} \leq x \leq \frac{\pi}{4}\] .
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
Check if the following relation is function:
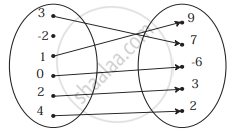
If f(m) = m2 − 3m + 1, find f(−3)
If f(m) = m2 − 3m + 1, find `f(1/2)`
Express the following logarithmic equation in exponential form
ln 1 = 0
Answer the following:
A function f is defined as f(x) = 4x + 5, for – 4 ≤ x < 0. Find the values of f(–1), f(–2), f(0), if they exist
Answer the following:
Find x, if x = 33log32
If the domain of function f(a) = a2 - 4a + 8 is (-∞, ∞), then the range of function is ______
Mapping f: R → R which is defined as f(x) = sin x, x ∈ R will be ______
