Advertisements
Advertisements
Question
Obtan an expression for potential energy of a particle performing S.H.M. What is the value of potential energy at (i) Mean position, and (ii) Extreme position
Solution
Potential Energy :
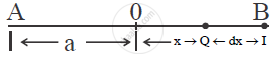
→ consider a particle of mass ‘m’ performing S.H.M along AB about mean position ‘O’.
→ OB = OA = a.
∴ When particle of mass ‘m’ performs S.H.M. is at distance x from its mean position.
→ Let ‘F = k x’ be the restoring force acting on the particle where k → force constant.
→ Let the particle is displaced by infinitesimal small distance 'dx'.
∴ Workdone,
dw = - fdx= -(-kx) dx= kxdx.
∴ total workdone is ,
`∫ dw= ∫ _(x=0)^x kxdx =k ∫ _(x=0)^x xdx`
`W = 1/2 kx^2= 1/2 mω^2x^2` `[∵ ω^2 = k/m]`
∴ this workdone is stored in the form of P.E.
∴ `P.E = 1/2 kx^2 = 1/2mω^2x^2`
Cases :
(i) at Mean position : - x = 0
∴ P.E = 0
(ii) at extreme position : x = ± a
∴ magnitude of P.E. is,
∴ `P.E =1/2 mω^2a^2`
APPEARS IN
RELATED QUESTIONS
Calculate the average molecular kinetic energy :
(a) per kilomole, (b) per kilogram, of oxygen at 27°C.
(R = 8320 J/k mole K, Avogadro's number = 6*03 x 1026 molecules/K mole)
Obtain an expression for potential energy of a particle performing simple harmonic motion. Hence evaluate the potential energy
- at mean position and
- at extreme position.
State an expression for K. E. (kinetic energy) and P. E. (potential energy) at displacement ‘x’ for a particle performing linear S.H. M. Represent them graphically. Find the displacement at which K. E. is equal to P. E.
Prove the law of conservation of energy for a particle performing simple harmonic motion.Hence graphically show the variation of kinetic energy and potential energy w. r. t. instantaneous displacement.
The kinetic energy of nitrogen per unit mass at 300 K is 2.5 × 106 J/kg. Find the kinetic energy of 4 kg oxygen at 600 K. (Molecular weight of nitrogen = 28, Molecular weight of oxygen = 32)
