Advertisements
Advertisements
Question
One says, "Give me a hundred, friend! I shall then become twice as rich as you". The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II)
[Hint: x + 100 = 2 (y − 100), y + 10 = 6(x − 10)]
Solution
Let those friends were having Rs x and y with them.
Using the information given in the question, we obtain
x + 100 = 2(y − 100)
x + 100 = 2y − 200
x − 2y = −300 (i)
And, 6(x − 10) = (y + 10)
6x − 60 = y + 10
6x − y = 70 (ii)
Multiplying equation (ii) by 2, we obtain
12x − 2y = 140 (iii)
Subtracting equation (i) from equation (iii), we obtain
11x = 140 + 300
11x = 440
x = 40
Using this in equation (i), we obtain
40 − 2y = −300
40 + 300 = 2y
2y = 340
y = 170
Therefore, those friends had Rs 40 and Rs 170 with them respectively.
APPEARS IN
RELATED QUESTIONS
Solve `\frac { 2 }{ x } + \frac { 1 }{ 3y } = \frac { 1}{ 5 }; \frac { 3 }{ x } + \frac { 2 }{ 3y } = 2` and also find ‘a’ for which y = ax – 2
Solve the following pairs of equations by reducing them to a pair of linear equations
`(7x-2y)/(xy) = 5`
`(8x + 7y)/(xy) = 15`
Solve the following pairs of equations by reducing them to a pair of linear equations
6x + 3y = 6xy
2x + 4y = 5xy
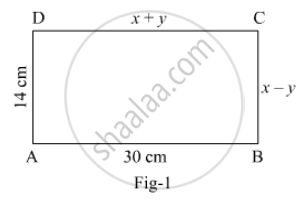
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
Find the value of following determinant.
`|(-1,7),(2,4)|`
The sum of digits of a two number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If 3 is added to the denominator and 2 is subtracted from the numerator, the fraction becomes `1/4`. Thus, we have
`(x-2)/(y+3)=1/4`
`⇒ 4(x-2)=y+3`
`⇒ 4x-8=y+3`
`⇒ 4x-y-11=0`
If 6 is added to the numerator and the denominator is multiplied by 3, the fraction becomes `2/3`. Thus, we have
`(x+6)/(3y)=2/3`
`⇒ 3(x+6)=6y`
`⇒ 3x +18 =6y`
`⇒ 3x-6y+18=0`
`⇒ 3(x-2y+6)=0`
`⇒ x-3y+6=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-1)xx6-(-2)xx(-11))=(-y)/(4xx6-1xx(-11))=1/(4xx(-2)-1xx(-1))`
`⇒ x/(-6-22)=-y/(24+11)=1/(-8+1)`
`⇒ x/-28=-y/35=1/-7`
`⇒ x= 28/7,y=35/7`
`⇒ x= 4,y=5`
Hence, the fraction is`4/5`
The present age of a father is three years more than three times the age of the son. Three years hence father's age will be 10 years more than twice the age of the son. Determine their present ages.
Father's age is three times the sum of age of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.
