Advertisements
Advertisements
Question
P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
Solution
Given: In a parallelogram ABCD, P is the mid-point of DC.
To prove: DA = AR and CQ = QR
Proof: ABCD is a parallelogram.
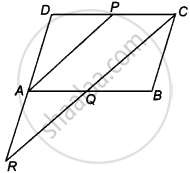
∴ BC = AD and BC || AD
Also, DC = AB and DC || AB
Since, P is the mid-point of DC.
∴ DP = PC = `1/2`DC
Now, QC || AP and PC || AQ
So, APCQ is a parallelogram
∴ AQ = PC = `1/2`DC
= `1/2`AB = BQ [∵ DC = AB] ...(i)
Now, in ΔAQR and ΔBQC,
AQ = BQ ...[From equation (i)]
∠AQR = ∠BQC ...[Vertically opposite angles]
And ∠ARQ = ∠BCQ ....[Alternate interior angles]
∴ ΔAQR = ΔBQC ...[By AAS congruence rule]
∴ AR = BC ...[By CPCT rule]
But BC = DA
∴ AR = DA
Also, CQ = QR ...[By CPCT rule]
Hence proved.
APPEARS IN
RELATED QUESTIONS
Diagonals of a parallelogram `square`WXYZ intersect each other at point O. If ∠XYZ = 135° then what is the measure of ∠XWZ and ∠YZW?
If l(OY)= 5 cm then l(WY)= ?
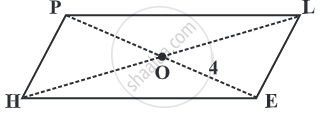
Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
Diagonals of a parallelogram are perpendicular to each other. Is this statement true? Give reason for your answer.
Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP = CQ (Figure). Show that AC and PQ bisect each other.
In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
If diagonals of a quadrilateral bisect each other, it must be a parallelogram.
The point of intersection of diagonals of a quadrilateral divides one diagonal in the ratio 1:2. Can it be a parallelogram? Why or why not?
Two sticks each of length 7 cm are crossing each other such that they bisect each other at right angles. What shape is formed by joining their end points? Give reason.
