Advertisements
Advertisements
Question
Peter throws two different dice together and finds the product of the two numbers obtained. Rina throws a die and squares the number obtained. Who has the better chance to get the number 25
Solution
Let us first write the all possible oucomes when Peter throws two different dice together.
(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
∴ Total number of outcomes = 36
The favorable outcome for getting the product of numbers on the dice equal to 25 is (5, 5).
Favourable number of outcomes = 1
∴ Probability that Peter gets the product of numbers as 25 = `"Favourable number of outcomes"/"Total number of outcomes" = 1/36`
The outcomes when Rina throws a die are 1, 2, 3, 4, 5, 6.
∴ Total number of outcomes = 6
Rina throws a die and squares the number, so to get the number 25, the favourable outcome is 5
Favourable number of outcomes = 1
∴ Probability that Rina gets the square of the number as 25 = `"Favourable number of outcomes"/"Total number of outcomes" = 1/6`
As `1/6 > 1/36`.so Rina has better chance to get the number 25.
APPEARS IN
RELATED QUESTIONS
A die is thrown once. Find the probability of getting a number between 3 and 6.
A letter of English alphabet is chosen at random. Determine the probability that the chosen letter is a consonant.
A child has a die whose 6 faces show the letters given below:
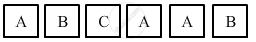
The die is thrown once. What is the probability of getting (i) A and (ii) B?
If the probability of winning a game is 0.7, what is the probability of losing it?
A box contains cards bearing numbers 6 to 70. If one card is drawn at random from the box, find the probability that it bears a number divisible by 5.
There are 25 tickets numbered 1, 2, 3, 4,..., 25 respectively. One ticket is draw at random. What is the probability that the number on the ticket is a multiple of 3 or 5?
The probability of getting 2 heads, when two coins are tossed, is
Two coins are tossed simultaneously. What is the probability of getting at most one head?
The probability of throwing a number greater than 2 with a fair die is
A child’s game has 8 triangles of which 3 are blue and rest are red and 10 squares of which 6 are blue and rest are red. One piece is lost at random. Find the probability that it is a triangle
