Advertisements
Advertisements
Question
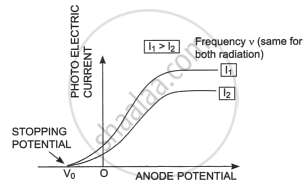
Plot a graph showing the variation of photoelectric current, as a function of anode potential for two light beams having the same frequency but different intensities I1 and I2 (I1 > I2). Mention its important features.
Solution
We use radiations with varying frequencies but the same intensity. When the frequency increases, the photoelectric current increases, and when the frequency decreases, the photoelectric current decreases. However, beyond a particular anode potential, the photoelectric current remains constant for all radiations of different frequencies. This is referred to as saturation current. As a result, the saturation current is unaffected by radiation frequency.
APPEARS IN
RELATED QUESTIONS
Define the term 'intensity of radiation' in terms of photon picture of light.
Every metal has a definite work function. Why do all photoelectrons not come out with the same energy if incident radiation is monochromatic? Why is there an energy distribution of photoelectrons?
It is found that yellow light does not eject photoelectrons from a metal. Is it advisable to try with orange light or with green light?
The threshold wavelength of a metal is λ0. Light of wavelength slightly less than λ0 is incident on an insulated plate made of this metal. It is found that photoelectrons are emitted for some time and after that the emission stops. Explain.
An atom absorbs a photon of wavelength 500 nm and emits another photon of wavelength 700 nm. Find the net energy absorbed by the atom in the process.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A sphere of radius 1.00 cm is placed in the path of a parallel beam of light of large aperture. The intensity of the light is 0.5 W cm−2. If the sphere completely absorbs the radiation falling on it, Show that the force on the sphere due to the light falling on it is the same even if the sphere is not perfectly absorbing.
The work function of a metal is 2.5 × 10−19 J. (a) Find the threshold frequency for photoelectric emission. (b) If the metal is exposed to a light beam of frequency 6.0 × 1014 Hz, what will be the stopping potential?
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
In an experiment on photoelectric effect, the stopping potential is measured for monochromatic light beams corresponding to different wavelengths. The data collected are as follows:-
Wavelength (nm): 350 400 450 500 550
Stopping potential (V): 1.45 1.00 0.66 0.38 0.16
Plot the stopping potential against inverse of wavelength (1/λ) on a graph paper and find (a) Planck's constant (b) the work function of the emitter and (c) the threshold wavelength.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
The electric field associated with a light wave is given by `E = E_0 sin [(1.57 xx 10^7 "m"^-1)(x - ct)]`. Find the stopping potential when this light is used in an experiment on photoelectric effect with the emitter having work function 1.9 eV.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
If photons of ultraviolet light of energy 12 eV are incident on a metal surface of work function of 4 eV, then the stopping potential (in eV) will be :
