Advertisements
Advertisements
Question
The work function of a metal is 2.5 × 10−19 J. (a) Find the threshold frequency for photoelectric emission. (b) If the metal is exposed to a light beam of frequency 6.0 × 1014 Hz, what will be the stopping potential?
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Solution
Given :-
Work function of a metal, W0 = 2.5 × 10−19 J
Frequency of light beam, v = 6.0 × 1014 Hz
(a) Work function of a metal,
W0 = hv0,
where h = Planck's constant
v0 = threshold frequency
`therefore "v"_0 = W_0/h`
`⇒ v_0 = (2.5 xx 10^-19)/(6.63 xx 10^-34)`
`= 3.77 xx 10^14 "Hz"`
`= 3.8 xx 10^14 "Hz"`
(b) Einstein's photoelectric equation :-
`eV_0 = hv - W_0`,
where
v = frequency of light
V0 = Stopping potential
e = charge on electron
`therefore V_0 = (hv - W_0)/e`
`= (6.63 xx 10^-34 xx 6 xx 10^14 - 2.5 xx 10^-19)/(1.6 xx 10^-19)`
`= (3.97 xx 10^-19 - 2.5 xx 10^-19)/(1.6 xx 10^-19) = 0.91 V`
APPEARS IN
RELATED QUESTIONS
A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ1 = 3650 Å, λ2 = 4047 Å, λ3 = 4358 Å, λ4 = 5461 Å, λ5 = 6907 Å,
The stopping voltages, respectively, were measured to be:
V01 = 1.28 V, V02 = 0.95 V, V03 = 0.74 V, V04 = 0.16 V, V05 = 0 V
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 × 10−19 C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
The work function for the following metals is given:
Na: 2.75 eV; K: 2.30 eV; Mo: 4.17 eV; Ni: 5.15 eV
Which of these metals will not give photoelectric emission for a radiation of wavelength 3300 Å from a He-Cd laser placed 1 m away from the photocell? What happens if the laser is brought nearer and placed 50 cm away?
Draw graphs showing variation of photoelectric current with applied voltage for two incident radiations of equal frequency and different intensities. Mark the graph for the radiation of higher intensity.
Can we find the mass of a photon by the definition p = mv?
What is the speed of a photon with respect to another photon if (a) the two photons are going in the same direction and (b) they are going in opposite directions?
The threshold wavelength of a metal is λ0. Light of wavelength slightly less than λ0 is incident on an insulated plate made of this metal. It is found that photoelectrons are emitted for some time and after that the emission stops. Explain.
If an electron has a wavelength, does it also have a colour?
Let nr and nb be the number of photons emitted by a red bulb and a blue bulb, respectively, of equal power in a given time.
The equation E = pc is valid
The work function of a metal is hv0. Light of frequency v falls on this metal. Photoelectric effect will take place only if
If the frequency of light in a photoelectric experiment is doubled, the stopping potential will ______.
If the wavelength of light in an experiment on photoelectric effect is doubled,
(a) photoelectric emission will not take place
(b) photoelectric emission may or may not take place
(c) the stopping potential will increase
(d) the stopping potential will decrease
Find the maximum kinetic energy of the photoelectrons ejected when light of wavelength 350 nm is incident on a cesium surface. Work function of cesium = 1.9 eV
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A small piece of cesium metal (φ = 1.9 eV) is kept at a distance of 20 cm from a large metal plate with a charge density of 1.0 × 10−9 C m−2 on the surface facing the cesium piece. A monochromatic light of wavelength 400 nm is incident on the cesium piece. Find the minimum and maximum kinetic energy of the photoelectrons reaching the large metal plate. Neglect any change in electric field due to the small piece of cesium present.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Explain how does (i) photoelectric current and (ii) kinetic energy of the photoelectrons emitted in a photocell vary if the frequency of incident radiation is doubled, but keeping the intensity same?
Show the graphical variation in the above two cases.
Consider a 20 W bulb emitting light of wavelength 5000 Å and shining on a metal surface kept at a distance 2 m. Assume that the metal surface has work function of 2 eV and that each atom on the metal surface can be treated as a circular disk of radius 1.5 Å.
- Estimate no. of photons emitted by the bulb per second. [Assume no other losses]
- Will there be photoelectric emission?
- How much time would be required by the atomic disk to receive energy equal to work function (2 eV)?
- How many photons would atomic disk receive within time duration calculated in (iii) above?
- Can you explain how photoelectric effect was observed instantaneously?
The graph shows the variation of photocurrent for a photosensitive metal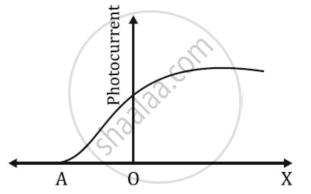
- What does X and A on the horizontal axis represent?
- Draw this graph for three different values of frequencies of incident radiation ʋ1, ʋ2 and ʋ3 (ʋ3 > ʋ2 > ʋ1) for the same intensity.
- Draw this graph for three different values of intensities of incident radiation I1, I2 and I3 (I3 > I2 > I1) having the same frequency.
Plot a graph showing the variation of photoelectric current, as a function of anode potential for two light beams having the same frequency but different intensities I1 and I2 (I1 > I2). Mention its important features.
