Advertisements
Advertisements
Question
Point P is at a distance of 6 cm from line AB. Draw a circle of radius 4 cm passing through point P so that line AB is the tangent to the circle
Solution
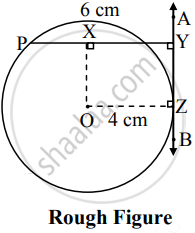
Analysis: As shown in the figure, A circle of radius 4 cm has center O.
Perpendicular distance of P from line AB = 6 cm.
∴ PY = 6 cm and ∠PYA = 90° ......(i)
seg OX is a perpendicular from point O to seg PY at point X.
Line AB is a tangent to the circle at point Z.
∴ OZ is radius of the circle.
In ▢XOZY,
∠X = 90° ......[∵ OX ⊥ PY]
∠Y = 90° ......[From (i)]
∠Z = 90° ......[Tangent theorem]
∴ ∠O = 90° ......[Remaning angle of ▢XOZY]
∴ ▢XOZY is a rectangle.
. ∴ seg ZY = seg OX and seg XO = seg YZ ......[Opposite sides of a rectangle]
But OZ = 4 cm ......…[Radius of the circle]
∴ XY = 4 cm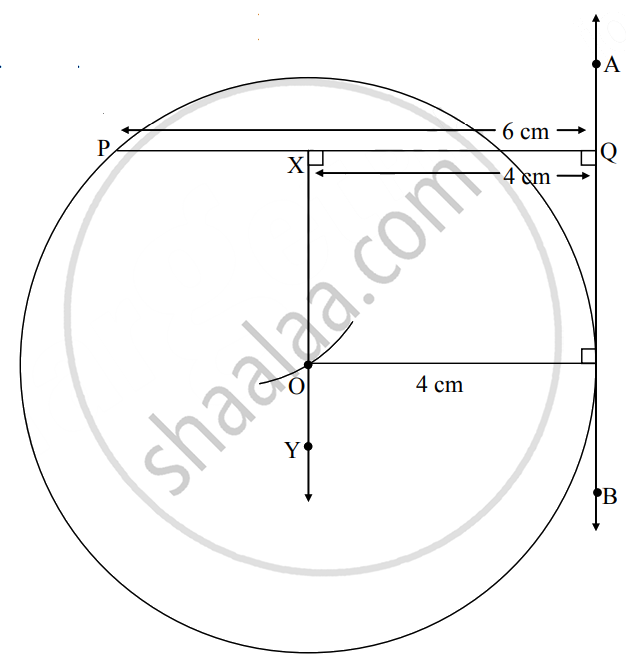
Steps of construction:
- Draw line AB.
- From any point Q on line AB, draw a, perpendicular PQ of 6 cm.
- Draw point X on seg PQ such that seg XQ = 4 cm.
- Draw ray XY interior of the circle such that ∠QXY = 90°
- Taking distance of 4 cm in compass, draw an arc with centre P on ray XY and name the point of intersection as O.
- With centre O, draw a circle of radius 4 cm. Which is the required circle.
APPEARS IN
RELATED QUESTIONS
ΔSHR ~ ΔSVU. In ΔSHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and `"SH"/("SV")=3/5`. Construct ΔSVU.
Draw ∠ABC of measure 105° and bisect it.
Draw `angle ABC` of measure 80° and bisect it
Draw ∠ABC of measures 135°and bisect it.

Observe the adjoining figure and write down one pair of interior angles.
If Δ ABC ∼ Δ XYZ then complete the following brackets.
`(AB)/(XY) = /(YZ) = (AC)/`
Draw ∠ ARP= 115° and bisect it.
Write down the equation of X- axis.
Draw ∠ABC of measure 120° and bisect it.
Prove that “That ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.”
Construct ∠ABC = 60° and bisect it
Construct ∠PQR = 115° and divide it into two equal parts
Draw Seg AB of length 9.7 cm. Take point P on it such that AP = 3.5 cm and A–P–B. Construct perpendicular to seg AB from point P.
Draw seg AB of length 4.5 cm and draw its perpendicular bisector
