Advertisements
Advertisements
Question
रेखा l रेखा m के समांतर है तथा एक तिर्यक रेखा p क्रमशः इन्हें X और Y पर प्रतिच्छेद करती है। X और Y पर स्थित अंतःकोणों के समद्विभाजक P और Q प्रतिच्छेद करते हैं। क्या PXQY एक आयत है? कारण दीजिए।
Solution
दिया गया है, l || m
अब, ∠DXY = ∠XYA ...[वैकल्पिक आंतरिक कोण]
⇒ `(∠DXY)/2 = (∠XYA)/2` ...[दोनों पक्षों को 2 से विभाजित करने पर]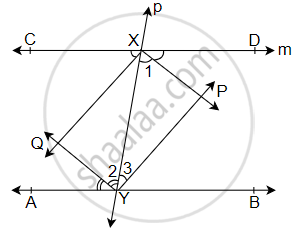
अब, ∠1 = ∠2 ...[एकांतर कोण बराबर हैं।]
XP और YQ समद्विभाजक हैं।
तो, XP || QY ...(i)
इसी तरह, XQ || PY ...(ii)
अब, समीकरण (i) और (ii) से हम पाते हैं।
समांतर चतुर्भुज PXQY में,
∠DXY + ∠XYB = 180° ...(iii) [तिर्यक रेखा के एक ही ओर के आंतरिक कोण संपूरक होते हैं।]
अब, दोनों पक्षों को 2 से विभाजित करके प्राप्त करें
`(∠DXY)/2 + (∠XYB)/2 = 180^circ/2`
तो, ∠1 + ∠3 = 90° [दोनों पक्षों को 2 से विभाजित करने पर] ...(iv)
त्रिभुज XYP में,
∠1 + ∠3 + ∠P = 180°
90° + ∠P = 180° ...[समीकरण (iv) से]
∠P = 180° – 90°
∠P = 90° ...(v)
समीकरण (iii) और (v) से,
PXQY एक आयत है।
APPEARS IN
RELATED QUESTIONS
एक चतुर्भुज का नाम बताइए जिसके विकर्ण बराबर हों।
निम्नलिखित के लिए कारण दीजिए:
वर्ग को एक विशेष प्रकार का आयत समझा जा सकता है।
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
यदि किसी चतुर्भुज के विकर्ण बराबर हों तथा परस्पर समद्विभाजित करें, तो वह होता है एक ______।
यदि किसी समांतर चतुर्भुज के आसन्न कोण बराबर हों, तो वह है एक –
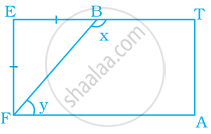
एक खेल का मैदान एक आयत ATEF के रूप का है। दो खिलाड़ी बिंदु F और B पर खड़ हैं, जहाँ EF = EB है। x और y के मान ज्ञात कीजिए।
एक आयत की रचना कीजिए, जिसकी एक भुजा 3 cm और विकर्ण 5 cm है।
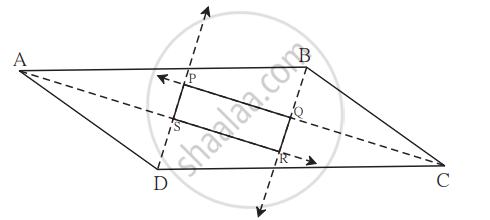
सिद्ध कीजिए कि, समांतर चतुर्भुज के चारों कोणों के समद्विभाजकों से बना चतुर्भुज आयत होता है।
आयत ABCD के विकर्ण परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। यदि AC = 8 सेमी तो BO = ? यदि ∠CAD = 35° तो ∠ACB = ?
नीचे दिए गए कथन सत्य हैं या असत्य, कारण सहित लिखिए।
प्रत्येक समांतर चतुर्भुज, आयत होता है।
