Advertisements
Advertisements
Question
Show how would you connect three resistors, each of resistance 6 O so that
the combination has a resistance of(a) 9 Ω (b) 4 .Ω
Solution
(a) To get an equivalent resistance of 9Ω using three 6 Ω resistors, they should be connected in parallel as shown:

Between A and C, the equivalent resistance is
`1/"R"_"parallel" = 1/6 + 1/6 = 2/6 = 1/3 Ω`
`"R"_"parallel" = 3 Ω
Between A and B, the equivalent resistance is
`"R"_"series" = 3 + 6 = 9Ω
(b) To get an equivalent resistance of 4 Ω using three 6 Ω resistors, they should be connected in parallel as shown:

Between A and B, the series combination of two 6 Ω resistors is connected in parallel with the third 6Ω resistor.
`"R"_"series" = 6 + 6 = 12Ω`
`1/"R"_"equivalent" = 1/6 + 1/12 = 3/12 = 1/4 Ω`
APPEARS IN
RELATED QUESTIONS
With a neat labelled diagram and derive the equation for three resistances connected in parallel.
A hot plate of an electric oven connected to a 220 V line has two resistance coils A and B, each of 24 Ω resistances, which may be used separately, in series, or in parallel. What are the currents in the three cases?
Show how would you join three resistors, each of resistance 9 Ω so that the equivalent resistance of the combination is
1) 13.5
2) 6 Ω
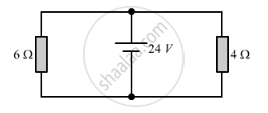
Find the current in each resistor in the circuit shown below:
An electric heater which is connected to a 220 V supply line has two resistance coils A and B of 24 Ω resistance each. These coils can be used separately (one at a time), in series or in parallel. Calculate the current drawn when:
(a) only one coil A is used.
(b) coils A and B are used in series.
(c) coils A and B are uses in parallel.
You are given three resistances of 1, 2 and 3 ohms. Shows by diagrams, how with the help of these resistances you can get:
(i) 6 Ω
(ii) `6/1` Ω
(iii) 1.5 Ω
Explain, why is the p.d. between the terminals of a storage battery less when it is supplying current than when it is on open circuit. A battery of e.m.f. 10 volts and internal resistance 2.5 ohms has two resistances of 50 ohms each connected to it. Calculate the power dissipated in each resistance
(a) When they are in series,
(b) When they are in parallel.
In each case calculate the power dissipated in the battery.
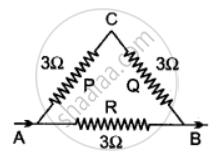
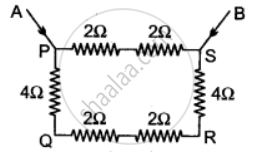
Calculate equivalent resistance in the following cases:
Two V-I graphs A and B for series and parallel combinations of two resistors are as shown. Giving reason state which graph shows (a) series, (b) parallel combination of the resistors.

Two resistors of resistances 2 Ω and 3 Ω are connected in parallel to a cell to draw current 0.5 A from the cell. Draw a labelled diagram of the arrangement
