Advertisements
Advertisements
Question
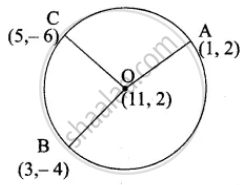
Show that the point (11, 2) is the centre of the circle passing through the points (1, 2), (3, −4) and (5, −6)
Solution
Distance = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
OA = `sqrt((11 - 1)^2 + (2 - 2)^2`
= `sqrt(10^2 + 0^2)`
= `sqrt(100)`
= 10
OB = `sqrt((11 - 3)^2 + (2 + 4)^2`
= `sqrt(8^2 + 6^2)`
= `sqrt(64 + 36)`
= `sqrt(100)`
= 10
OC = `sqrt((11 - 5)^2 + (2 + 6)^2`
= `sqrt(6^2 + 8^2)`
= `sqrt(36 + 64)`
= `sqrt(100)`
= 10
OA = OB = OC = 10
O is the centre of the circle passing through A, B and C.
APPEARS IN
RELATED QUESTIONS
If the co-ordinate of A is x and that of B is y, find d(A, B).
x = 4, y = - 8
On a number line, co-ordinates of P, Q, R are 3, -5 and 6 respectively. State with reason whether the following statement is true or false.
d(P, R) + d(R, Q) = d(P, Q)
Co-ordinates of the pair of a point is given below. Hence find the distance between the pair.
3, 6
Co-ordinates of the pair of points are given below. Hence find the distance between the pair.
- 25, - 47
Co-ordinates of the pair of points are given below. Hence find the distance between the pair.
80, - 85
Find the distance between the following pair of points
(a, b) and (c, b)
Show that the following points taken in order to form an isosceles triangle
A(5, 4), B(2, 0), C(−2, 3)
Find the distance with the help of the number line given below.

d(B, E)
Find the distance with the help of the number line given below.

d(J, H)
Find the distance with the help of the number line given below.

d(K, O)
