Advertisements
Advertisements
Question
सिद्ध कीजिए कि एक समांतर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
Solution
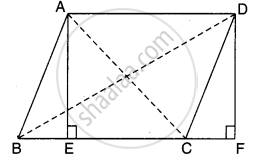
मान लीजिए ABCD एक समान्तर चतुर्भुज है। A से AE ⊥ BC एवं D से DF ⊥ BC खींचिए। ABCD के विकर्ण AC और BD हैं। यहाँ AEFD एक आयत है।
समकोण ∆AEB और ∆DFC में,
∵ कर्ण AB = कर्ण DC
[समान्तर चतुर्भुज की सम्मुख भुजाएँ]
∵ भुजा AE = भुजा DF [आयत की सम्मुख भुजाएँ हैं]
⇒ ∆AEB ≅ ∆DFC [RHS सर्वांगसमता]
⇒ BE = CF …(1) [CPCT]
अधिककोण ∆DCB में ∠DCB अधिककोण है
⇒ BD2 = BC2 + CD2 + 2BC.CF .....(2) [अधिककोण उपप्रमेय से]
∵ न्यूनकोण ∆ABC में ∠ABC न्यूनकोण है
⇒ AC2 = AB2 + BC2 – 2 BE.BC [न्यूनकोण उपप्रमेय से]
⇒ AC2 = AB2 + DA2 – 2 BC.CF …(3)
[∵ BE = CF समीकरण (1) तथा BC = AD समान्तर ABCD की सम्मुख भुजाएँ हैं।]
⇒ AC2 + BD2 = AB2 + DA2 + BC2 + CD2
[समीकरण (2) + समीकरण (3) से]
⇒ AC2 + BD2 = AB2 + BC2 + CD2 + DA2
अतः किसी समान्तर चतुर्भुज में उसके विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
इति सिद्धम्
APPEARS IN
RELATED QUESTIONS
निम्नलिखित युग्म के दो भिन्न-भिन्न उदाहरण दीजिए:
समरूप आकृतियाँ
निम्नलिखित युग्म के दो भिन्न-भिन्न उदाहरण दीजिए:
ऐसी आकृतियाँ जो समरूप नहीं हैं।
बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं:

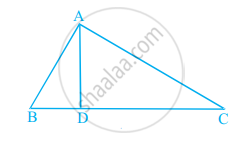
आकृति में, ∠BAC = 90° और AD ⊥ BC हैं। तब, ______।
एक समचतुर्भुज के विकर्णों की लंबाइयाँ 16 cm और 12 cm हैं। तब इस समचतुर्भुज की भुजा की लंबाई ______ है।
