Advertisements
Advertisements
Question
Solve –12x > 30, when x is a natural number.
Solution
The given inequality is -12x > 30.
- 12x > 30
⇒ `(-12x)/(-12) < 30/(-12)` (dividing both sides by same negative number)
⇒ x < `- 5/2`
There is no natural number less than (-5/2).
Thus, when x is a natural number, the given inequality has no solution.
APPEARS IN
RELATED QUESTIONS
Solve 24x < 100, when x is a natural number.
Solve 5x – 3 < 7, when x is an integer.
Solve the given inequality for real x: 4x + 3 < 5x + 7.
Solve the given inequality for real x: 3x – 7 > 5x – 1.
Solve the given inequality for real x: 3(x – 1) ≤ 2 (x – 3)
Solve the given inequality for real x: x + `x/2` + `x/3` < 11
Solve the given inequality for real x : `x/3 > x/2 + 1`
Solve the given inequality for real x : `(3(x-2))/5 <= (5(2-x))/3`
Solve the given inequality for real x: `1/2 ((3x)/5 + 4) >= 1/3 (x -6)`
Solve the given inequality for real x: 37 – (3x + 5) ≥ 9x – 8(x – 3)
Solve the given inequality for real x: `x/4 < (5x - 2)/3 - (7x - 3)/5`
Solve the given inequality and show the graph of the solution on number line:
3x – 2 < 2x +1
Solve the given inequality and show the graph of the solution on number line:
5x – 3 ≥ 3x – 5
Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.
A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 3 cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5 cm longer than the second?
[Hint: If x is the length of the shortest board, then x, (x + 3) and 2x are the lengths of the second and third piece, respectively. Thus, x = (x + 3) + 2x ≤ 91 and 2x ≥ (x + 3) + 5]
Solve the inequality.
6 ≤ –3(2x – 4) < 12
Solve the inequality.
`-15 < (3(x - 2))/5 <= 0`
Solve the inequality.
`-12 < 4 - (3x)/(-5) <= 2`
Solve the inequality.
`7 <= (3x + 11)/2 <= 11`
Represent to solution set of each of the following inequations graphically in two dimensional plane:
x + 2 ≥ 0
Represent to solution set of each of the following inequations graphically in two dimensional plane:
6. x ≤ 8 − 4y
Represent to solution set of each of the following inequations graphically in two dimensional plane:
0 ≤ 2x − 5y + 10
Represent to solution set of each of the following inequations graphically in two dimensional plane:
3x − 2y ≤ x + y − 8
State whether the following statement is True or False.
If xy > 0, then x > 0, and y < 0
State whether the following statement is True or False.
If xy < 0, then x > 0, and y > 0
State whether the following statement is True or False.
If |x| < 5, then x ∈ (–5, 5)
The inequality representing the following graph is ______.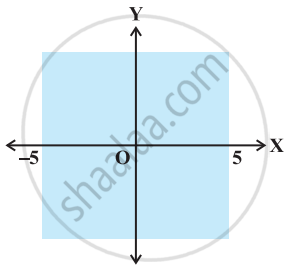
Solution of a linear inequality in variable x is represented on number line given below ______.
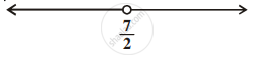
Solution of a linear inequality in variable x is represented on number line given below ______.

If x > –2 and x < 9, then x ∈ (– 2, 9)
If |x| > 5, then x ∈ (– `oo`, – 5) ∪ [5, `oo`)
