Advertisements
Advertisements
Question
Represent to solution set of each of the following inequations graphically in two dimensional plane:
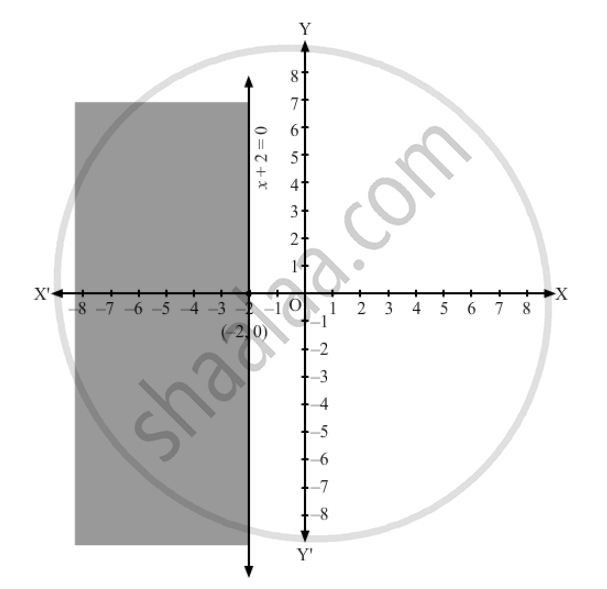
x + 2 ≥ 0
Solution
Converting the inequation to equation, we obtain x + 2 = 0, i.e x = \[-\] Clearly, it is a parallel line to y-axis at a distance of \[-\]2 units from it. This line divides the xy plane into two parts, viz LHS of x =\[-\] 2 and RHS of x = \[-\] 2. To determine the region represented by the given inequality, consider point O(0,0). Clearly, (0,0) does not satisfy the inequality. So, the region that does not contain the origin is represented by the given inequality.
Hence, the shaded region is the solution to the inequation.
APPEARS IN
RELATED QUESTIONS
Solve –12x > 30, when x is a natural number.
Solve –12x > 30, when x is an integer.
Solve 5x – 3 < 7, when x is a real number.
Solve 3x + 8 > 2, when x is an integer.
Solve 3x + 8 > 2, when x is a real number.
Solve the given inequality for real x: 4x + 3 < 5x + 7.
Solve the given inequality for real x: 3x – 7 > 5x – 1.
Solve the given inequality for real x: 3(x – 1) ≤ 2 (x – 3)
Solve the given inequality for real x : `x/3 > x/2 + 1`
Solve the given inequality for real x: `x/4 < (5x - 2)/3 - (7x - 3)/5`
Solve the given inequality for real x: `((2x- 1))/3 >= ((3x - 2))/4 - ((2 - x))/5`
Solve the given inequality and show the graph of the solution on number line:
3x – 2 < 2x +1
To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.
Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.
Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.
Solve the inequality.
6 ≤ –3(2x – 4) < 12
Solve the inequality.
`-3 <= 4 - (7x)/2 <= 18`
Solve the inequality.
`-15 < (3(x - 2))/5 <= 0`
Represent to solution set of each of the following in equations graphically in two dimensional plane:
2. x + 2y ≥ 6
Represent to solution set of each of the following inequations graphically in two dimensional plane:
4. x − 2y < 0
Represent to solution set of each of the following inequations graphically in two dimensional plane:
5. −3x + 2y ≤ 6
Represent to solution set of each of the following inequations graphically in two dimensional plane:
6. x ≤ 8 − 4y
Represent to solution set of each of the following inequations graphically in two dimensional plane:
3y ≥ 6 − 2x
Represent to solution set of each of the following inequations graphically in two dimensional plane:
y ≥ 2x − 8
State whether the following statement is True or False.
If x > y and b < 0, then bx < by
State whether the following statement is True or False.
If xy > 0, then x > 0, and y < 0
State whether the following statement is True or False.
Solution set of x – y ≤ 0 is
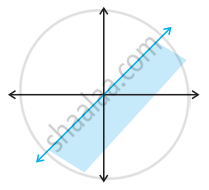
The inequality representing the following graph is ______.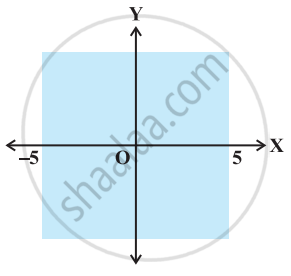
Solution of a linear inequality in variable x is represented on number line given below ______.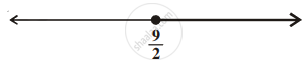
Solution of a linear inequality in variable x is represented on number line given below ______.
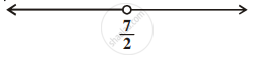
If x > –2 and x < 9, then x ∈ (– 2, 9)
If |x| ≤ 4, then x ∈ [– 4, 4]
