Advertisements
Advertisements
Question
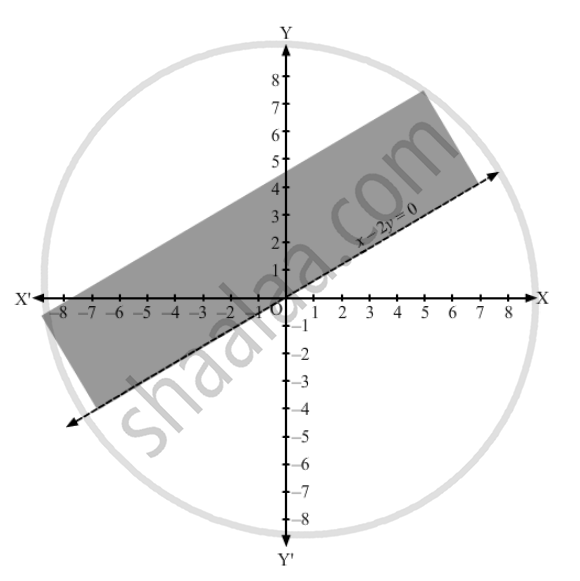
Represent to solution set of each of the following inequations graphically in two dimensional plane:
4. x − 2y < 0
Solution
Converting the inequation to equation, we obtain x \[-\] 2y =0
Putting y = 0 and x = 0 in this equation, we obtain x = 0 and y = 0 respectively. So, this line meets the x-axis at (0,0) and the y- axis at (0,0).
If x = 1, then y = 1/2.
So, we have another point (1,1/2).
We plot these points and join them by a thin line. This divides the xy plane into two parts.
We take a point (0, 2) and it does not satisfy the inequation.
Therefore, we shade the region which is opposite to the point (0, 2)
The shaded region is the solution to the inequation.
APPEARS IN
RELATED QUESTIONS
Solve 24x < 100, when x is a natural number.
Solve 24x < 100, when x is an integer.
Solve –12x > 30, when x is a natural number.
Solve –12x > 30, when x is an integer.
Solve the given inequality for real x: 3x – 7 > 5x – 1.
Solve the given inequality for real x: 3(x – 1) ≤ 2 (x – 3)
Solve the given inequality for real x: x + `x/2` + `x/3` < 11
Solve the given inequality for real x : `x/3 > x/2 + 1`
Solve the given inequality for real x: `(3(x-2))/5 <= (5(2-x))/3`
Solve the given inequality for real x : `(3(x-2))/5 <= (5(2-x))/3`
Solve the given inequality for real x: `1/2 ((3x)/5 + 4) >= 1/3 (x -6)`
Solve the given inequality for real x: 37 – (3x + 5) ≥ 9x – 8(x – 3)
Solve the given inequality for real x: `((2x- 1))/3 >= ((3x - 2))/4 - ((2 - x))/5`
Solve the given inequality and show the graph of the solution on number line:
3x – 2 < 2x +1
Solve the given inequality and show the graph of the solution on number line:
`x/2 >= ((5x -2))/3 - ((7x - 3))/5`
Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.
Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.
Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.
Solve the inequality.
`-3 <= 4 - (7x)/2 <= 18`
Solve the inequality.
`-15 < (3(x - 2))/5 <= 0`
Solve the inequality.
`-12 < 4 - (3x)/(-5) <= 2`
Solve the inequality.
`7 <= (3x + 11)/2 <= 11`
Represent to solution set of each of the following inequations graphically in two dimensional plane:
x + 2y − y ≤ 0
Represent to solution set of each of the following in equations graphically in two dimensional plane:
2. x + 2y ≥ 6
Represent to solution set of each of the following inequations graphically in two dimensional plane:
x + 2 ≥ 0
Represent to solution set of each of the following inequations graphically in two dimensional plane:
6. x ≤ 8 − 4y
Represent to solution set of each of the following inequations graphically in two dimensional plane:
3y ≥ 6 − 2x
Represent to solution set of each of the following inequations graphically in two dimensional plane:
y ≥ 2x − 8
Represent to solution set of each of the following inequations graphically in two dimensional plane:
3x − 2y ≤ x + y − 8
State whether the following statement is True or False.
If x > y and b < 0, then bx < by
State whether the following statement is True or False.
If xy < 0, then x > 0, and y > 0
Solution of a linear inequality in variable x is represented on number line given below ______.

Solution of a linear inequality in variable x is represented on number line given below ______.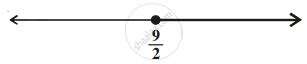
Solution of a linear inequality in variable x is represented on number line given below ______.

If x > –2 and x < 9, then x ∈ (– 2, 9)
