Advertisements
Advertisements
Question
Solve the given inequality for real x : `x/3 > x/2 + 1`
Solution
The given inequality `x/3 > x/2 + 1`
`x/3 - x/2 > 1`
or `(2x - 3x)/6 > 1`
= `-x/6 > 1`
-On multiplying by 6,
x < - 6
Thus, all real numbers x, which are less than -6, are the solutions of the given inequality.
Hence, the solution set of the given inequality is (–∞, –6).
APPEARS IN
RELATED QUESTIONS
Solve 24x < 100, when x is a natural number.
Solve –12x > 30, when x is an integer.
Solve 5x – 3 < 7, when x is an integer.
Solve 3x + 8 > 2, when x is an integer.
Solve 3x + 8 > 2, when x is a real number.
Solve the given inequality for real x: 4x + 3 < 5x + 7.
Solve the given inequality for real x: 3(x – 1) ≤ 2 (x – 3)
Solve the given inequality for real x: 3(2 – x) ≥ 2(1 – x)
Solve the given inequality for real x: x + `x/2` + `x/3` < 11
Solve the given inequality for real x: 2(2x + 3) – 10 < 6 (x – 2)
Solve the given inequality for real x: 37 – (3x + 5) ≥ 9x – 8(x – 3)
Solve the given inequality for real x: `((2x- 1))/3 >= ((3x - 2))/4 - ((2 - x))/5`
Solve the given inequality and show the graph of the solution on number line:
5x – 3 ≥ 3x – 5
Solve the given inequality and show the graph of the solution on number line:
3(1 – x) < 2 (x + 4)
Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.
The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
Solve the inequality.
`-3 <= 4 - (7x)/2 <= 18`
Solve the inequality.
`-15 < (3(x - 2))/5 <= 0`
Solve the inequality.
`-12 < 4 - (3x)/(-5) <= 2`
Represent to solution set of each of the following in equations graphically in two dimensional plane:
2. x + 2y ≥ 6
Represent to solution set of each of the following inequations graphically in two dimensional plane:
x + 2 ≥ 0
Represent to solution set of each of the following inequations graphically in two dimensional plane:
4. x − 2y < 0
Represent to solution set of each of the following inequations graphically in two dimensional plane:
0 ≤ 2x − 5y + 10
Represent to solution set of each of the following inequations graphically in two dimensional plane:
3y ≥ 6 − 2x
Represent to solution set of each of the following inequations graphically in two dimensional plane:
y ≥ 2x − 8
Represent to solution set of each of the following inequations graphically in two dimensional plane:
3x − 2y ≤ x + y − 8
State whether the following statement is True or False.
If x > 5 and x > 2, then x ∈ (5, ∞)
State whether the following statement is True or False.
If |x| < 5, then x ∈ (–5, 5)
The inequality representing the following graph is ______.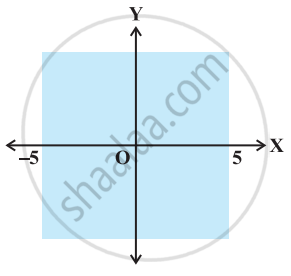
Solution of a linear inequality in variable x is represented on number line given below ______.

Solution of a linear inequality in variable x is represented on number line given below ______.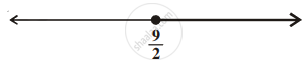
If |x| > 5, then x ∈ (– `oo`, – 5) ∪ [5, `oo`)
