Advertisements
Advertisements
Question
Solve graphically : 2y – 5 ≥ 0
Solution
Consider the line whose equation is 2y – 5 = 0, i.e. y = `(5)/(2)`
This represents a line parallel to X-axis passing5through the point `(0, 5/2)`
Draw the line y = `(5)/(2)`.
To find the solution set, we have to check the position of the origin (0, 0).
When y = 0, 2y – 5 = 2 x – 5 = –5 `cancel>=` 0
∴ the coordinates of the origin does not satisfy the given inequality.
∴ the solution set consists of the line y == `(5)/(2)` and the non-origin side of the line which is shaded in the graph.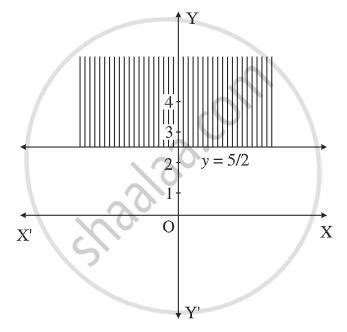
APPEARS IN
RELATED QUESTIONS
Solve graphically: x ≥ 0
Solve graphically : y ≥ 0
Solve graphically : x ≥ 0 and y ≥ 0
Solve graphically : x ≥ 0 and y ≤ 0.
Solve graphically : 3x + 4 ≤ 0
Solve graphically : 5y + 3 ≤ 0
Solve graphically : x +2y ≤ 6
Solve graphically : 5x – 3y ≤ 0
Solve graphically : 2x + y ≥ 2 and x – y ≤ 1
Solve graphically : x + y ≥ 6 and x + 2y ≤ 10
The corner points of the feasible solutions are (0, 0) (3, 0) (2, 1) (0, 7/3) the maximum value of Z = 4x + 5y is
The half plane represented by 4x + 3y >14 contains the point
The value of objective function is maximum under linear constraints
If a corner point of the feasible solutions are (0, 10) (2, 2) (4, 0) (3, 2) then the point of minimum Z = 3x + 2y is
Check the ordered points (1, −1), (2, −1) is a solution of 2x + 3y − 6 ≤ 0
Show the solution set of inequations 4x – 5y ≤ 20 graphically
If the point (x1, y1) satisfies px - qy < 13, then the solution set represented by the inequation is ______
For the constraint of a linear optimizing function z = 3x1 + 11x2, given by 2x1 + x2 ≤ 2, 4x1 + x2 ≥ 4 and x1, x2 ≥ 0
Let p and q be the statements:
p: 3x3 + 8y3 ≥ 15, q: 5x + 2y < 11
Then, which of the following is true?
Solution of the LPP minimize z = 7x + 2y subject to x + y ≥ 60, x - 2y ≥ 0, x + 2y ≤ 120, x, y ≥ 0 is ______
The maximum value of z = 7x + 6y.
Subject to the constraints x ≤ 45, y ≤ 55 and x ≥ 0, y ≥ 0 is ______.
Region represented by the inequalities x ≥ 0, y ≤ 0 is ______.
Determine the system of linear equation for which the solution set is the shaded region in the following figure ______.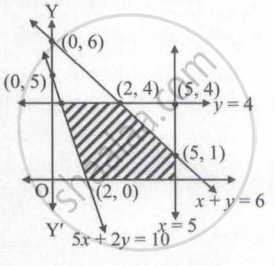
Solution set of the inequality y ≥ 0 is ______.
Which of the following linear inequalities satisfy the shaded region of the given figure?
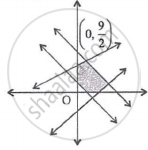
The objective function of LPP defined over the convex set attains it optimum value at ______.
