Advertisements
Advertisements
Question
Show the solution set of inequations 4x – 5y ≤ 20 graphically
Solution
| Given inequality | 4x – 5y ≤ 20 |
| Corresponding equality | 4x – 5y = 20 |
| Intersection of line with X-axis | A(5, 0) |
| Intersection of line with Y-axis | B(0, – 4) |
| Origin test | 4(0) – 5(0) ≤ 20 i.e., 0 ≤ 20 which is true |
| Region | Origin side of the line |
The shaded portion represents the graphical solution.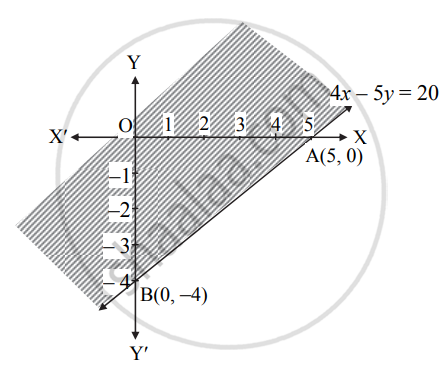
APPEARS IN
RELATED QUESTIONS
Solve graphically: x ≥ 0
Solve graphically : x ≤ 0
Solve graphically: x ≤ 0 and y ≥ 0
Solve graphically : x ≤ 0 and y ≤ 0
Solve graphically : x ≥ 0 and y ≤ 0.
Solve graphically: 2x – 3 ≥ 0
Solve graphically : 2y – 5 ≥ 0
Solve graphically : 3x + 4 ≤ 0
Solve graphically : 5y + 3 ≤ 0
Solve graphically : x +2y ≤ 6
Solve graphically : 2x – 5y ≥10
Solve graphically: 3x + 2y ≥ 0
Solve graphically : 5x – 3y ≤ 0
Solve graphically : x + y ≥ 6 and x + 2y ≤ 10
Solve graphically : 2x + y ≥ 5 and x – y ≤ 1
The corner points of the feasible solutions are (0, 0) (3, 0) (2, 1) (0, 7/3) the maximum value of Z = 4x + 5y is
Check the ordered points (1, −1), (2, −1) is a solution of 2x + 3y − 6 ≤ 0
If the point (x1, y1) satisfies px - qy < 13, then the solution set represented by the inequation is ______
For the constraint of a linear optimizing function z = 3x1 + 11x2, given by 2x1 + x2 ≤ 2, 4x1 + x2 ≥ 4 and x1, x2 ≥ 0
Let p and q be the statements:
p: 3x3 + 8y3 ≥ 15, q: 5x + 2y < 11
Then, which of the following is true?
Solution of the LPP minimize z = 7x + 2y subject to x + y ≥ 60, x - 2y ≥ 0, x + 2y ≤ 120, x, y ≥ 0 is ______
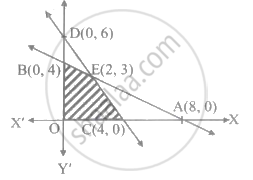
The shaded region is represented by the in equations ______
If S1 and S2 are respectively the sets of local minimum and local maximum points of the function, f(x) = 9x4 + 12x3 - 36x2 + 25, x ∈ R, then ______
Solution set of the inequality y ≥ 0 is ______.
The set of real x satisfying the inequality `(5 - 2x)/3 ≤ x/6 - 5` is [a, ∞). The value of ‘a’ is ______.
Which of the following linear inequalities satisfy the shaded region of the given figure?
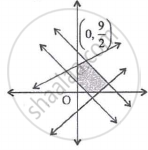
The objective function of LPP defined over the convex set attains it optimum value at ______.
