Advertisements
Advertisements
Question
Solve graphically: 3x + 2y ≥ 0
Solution
Consider the line whose equation is 3x + 2y = 0. The constant term is zero, therefore this line is passing through the origin.
∴ One point on the line is O = (0, 0).
To find another point, we can give any value of x and get the corresponding value of y.
Put x = 2, we get 6 + 2y = 0 i.e. y = –3
∴ A = (2, –3), is another point on the line. Draw the line OA.
To find the solution set, we cannot check (0,0) as it is already on the line.
We can check any other point which is not on the line.
Let us check the point (1, 1).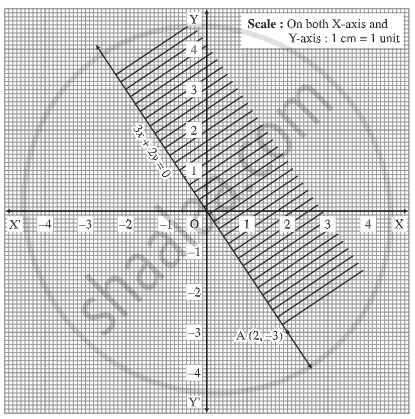
When x = 1, y = 1, then 3x + 2y = 3 + 2 = 5 which is grreater than zer.
∴ 3x + 2y > 0 in this case.
Hence (1, 1) lies in the required region.
Therefore, the required region is the upper side which is shaded in the graph.
This is the solution set of x + 2y > 0.
RELATED QUESTIONS
Solve graphically: x ≥ 0
Solve graphically : y ≥ 0
Solve graphically : x ≤ 0
Solve graphically : x ≥ 0 and y ≥ 0
Solve graphically: x ≤ 0 and y ≥ 0
Solve graphically : x ≤ 0 and y ≤ 0
Solve graphically: 2x – 3 ≥ 0
Solve graphically : 2y – 5 ≥ 0
Solve graphically : 3x + 4 ≤ 0
Solve graphically : 5y + 3 ≤ 0
Solve graphically : 2x + y ≥ 2 and x – y ≤ 1
Solve graphically : x – y ≤ 2 and x + 2y ≤ 8
Solve graphically : 2x + 3y≤ 6 and x + 4y ≥ 4
Solve graphically : 2x + y ≥ 5 and x – y ≤ 1
The corner points of the feasible solutions are (0, 0) (3, 0) (2, 1) (0, 7/3) the maximum value of Z = 4x + 5y is
The half plane represented by 4x + 3y >14 contains the point
If a corner point of the feasible solutions are (0, 10) (2, 2) (4, 0) (3, 2) then the point of minimum Z = 3x + 2y is
A solution set of the inequality x ≥ 0
Show the solution set of inequations 4x – 5y ≤ 20 graphically
If the point (x1, y1) satisfies px - qy < 13, then the solution set represented by the inequation is ______
Let p and q be the statements:
p: 3x3 + 8y3 ≥ 15, q: 5x + 2y < 11
Then, which of the following is true?
The shaded region is represented by the in equations ______
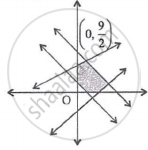
If S1 and S2 are respectively the sets of local minimum and local maximum points of the function, f(x) = 9x4 + 12x3 - 36x2 + 25, x ∈ R, then ______
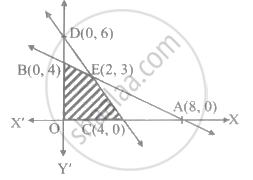
Determine the system of linear equation for which the solution set is the shaded region in the following figure ______.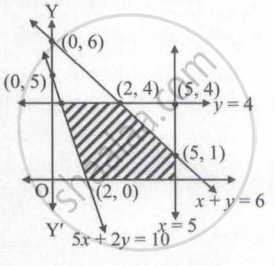
The set of real x satisfying the inequality `(5 - 2x)/3 ≤ x/6 - 5` is [a, ∞). The value of ‘a’ is ______.
Which of the following linear inequalities satisfy the shaded region of the given figure?
The object function z = 4x1 + 5x2, subject to 2x1 + x2 ≥ 7, 2x1 + 3x2 ≤ 15, x2 ≤ 3, x1, x2 ≥ 0 has minimum value at the point is ______.
The objective function of LPP defined over the convex set attains it optimum value at ______.
