Advertisements
Advertisements
Question
Solve the following problem.
A 2 m long wooden plank of mass 20 kg is pivoted (supported from below) at 0.5 m from either end. A person of mass 40 kg starts walking from one of these pivots to the farther end. How far can the person walk before the plank topples?
Solution
Let the person starts walking from pivot P2 as shown in the figure.
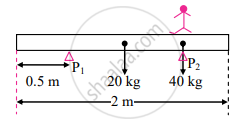
Assume the person can walk up to distance x from P1 before the plank topples. The plank will topple when the moment exerted by the person about P1 is not balanced by a moment of force due to plank about P2.
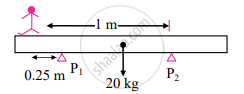
∴ For equilibrium,
40 × x = 20 × 0.5
∴ x = `1/4` = 0.25 m
Hence, the total distance walked by the person is 1.25 m.
APPEARS IN
RELATED QUESTIONS
Explain balancing or mechanical equilibrium. The linear velocity of a rotating fan as a whole is generally zero. Is it in mechanical equilibrium? Justify your answer.
Solve the following problem.
A 2 m long ladder of mass 10 kg is kept against a wall such that its base is 1.2 m away from the wall. The wall is smooth but the ground is rough. The roughness of the ground is such that it offers a maximum horizontal resistive force (for sliding motion) half that of normal reaction at the point of contact. A monkey of mass 20 kg starts climbing the ladder. How far can it climb along the ladder? How much is the horizontal reaction at the wall?
A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is ____________.
A uniform bar RS weighs 100 g and is 80 cm long. From the end R, two masses 50 g and 100 g are hung from the bar at a distance of 10 cm and 60 cm respectively. If the bar is to remain horizontal when balanced on a knife-edge, its position is ____________.
5 m long see-saw remains horizontal when two children weighing 20 kg and 30 kg respectively sit at two ends. Where is the see-saw supported?
A see-saw of length 6 m is pivoted at its centre. A child of mass 20 kg is sitting at one of its ends. Where should another child, of mass 30 kg, sit on the other end from the centre of see-saw, so that it is balanced?
