Advertisements
Advertisements
Question
Solve the following quadratic equation by factorisation method:
x2 + x – 20 = 0
Solution
x2 + x – 20 = 0
∴ x2 + 5x − 4x − 20 = 0
∴ x + 5x – 4x − 20 = 0
∴ x(x + 5) – 4(x + 5) = 0
∴ (x + 5)(x – 4) = 0
∴ (x + 5) = 0 or (x – 4) = 0
∴ x + 5 = 0 or x – 4 = 0
∴ x = – 5 or x = 4
∴ – 5 and 4 are roots of the given quadratic equation.
RELATED QUESTIONS
Solve for x :
`2/(x+1)+3/(2(x-2))=23/(5x), x!=0,-1,2`
Solve the following quadratic equations by factorization:
`x^2-4sqrt2x+6=0`
Solve the following quadratic equations by factorization:
`(2x)/(x-4)+(2x-5)/(x-3)=25/3`
Solve the following quadratic equations by factorization:
a2b2x2 + b2x - a2x - 1 = 0
The product of Shikha's age five years ago and her age 8 years later is 30, her age at both times being given in years. Find her present age.
`x^2-4x+1=0`
The sum of the squares of two consecutive positive integers is 365. Find the integers.
The distance between Akola and Bhusawal is 168 km. An express train takes 1 hour less than a passenger train to cover the distance. Find the average speed of each train if the average speed of the express train is more by 14 km/hr than the speed of the passenger train.
Solve the following quadratic equations by factorization: \[\sqrt{3} x^2 - 2\sqrt{2}x - 2\sqrt{3} = 0\]
If the equation x2 + 4x + k = 0 has real and distinct roots, then
If x = 1 is a common roots of the equations ax2 + ax + 3 = 0 and x2 + x + b = 0, then ab =
If a and b can take values 1, 2, 3, 4. Then the number of the equations of the form ax2 +bx + 1 = 0 having real roots is
Find two natural numbers which differ by 3 and whose squares have the sum of 117.
Solve the following equation by factorization
3x2 – 5x – 12 = 0
Solve the following equation by factorization
x(6x – 1) = 35
Solve the following equation by factorization
`(8)/(x + 3) - (3)/(2 - x)` = 2
Solve the following equation by factorization
`(x - 3)/(x + 3) + (x + 3)/(x - 3) = 2(1)/(2)`
Car A travels x km for every litre of petrol, while car B travels (x + 5) km for every litre of petrol.
(i) Write down the number of litres of petrol used by car A and car B in covering a distance of 400 km.
(ii) If car A uses 4 litres of petrol more than car B in covering 400 km. write down an equation, in A and solve it to determine the number of litres of petrol used by car B for the journey.
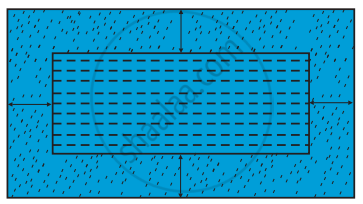
In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m2 [see figure]. Find the length and breadth of the pond.