Advertisements
Advertisements
Question
Study the two circuits shown in the figure below. The cells in the two circuits are identical to each other. The resistance of the load resistor R is the same in both circuits.
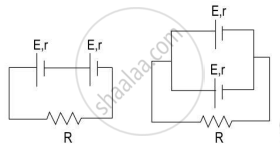
If the same current flows through the resistor R in both circuits, calculate the internal resistance of each cell in terms of the resistance of resistor R. Show your calculations.
Solution
Current I in load resistance R is given by the formula,
I = `"E"/("R"+"r")`;
where E is the emf of the cell,
r is the internal resistance of the cell.
In circuit 1, the cells are in series.
∴ Eeq = 2E and req = 2r
Current through R in circuit 1, I = `(2"E")/(("R"+2"r"))`
In circuit 2, the cells are in parallel.
∴ Eeq = E and req = `"r"/2`
Current through R in circuit 2, I = `"E"/(("R"+"r"/2))`
Since the current is the same in both circuits,
`(2"E")/ (("R"+2"r")) = "E"/(("R"+"r"/2))`
Solving, we get r = R
APPEARS IN
RELATED QUESTIONS
Two cells of emfs 1.5 V and 2.0 V, having internal resistances 0.2 Ω and 0.3 Ω, respectively, are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
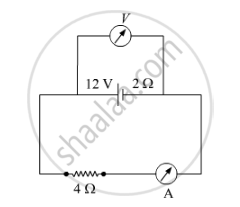
A battery of emf 12 V and internal resistance 2 Ω is connected to a 4 Ω resistor as shown in the figure.
(a) Show that a voltmeter when placed across the cell and across the resistor, in turn, gives the same reading.
(b) To record the voltage and the current in the circuit, why is voltmeter placed in parallel and ammeter in series in the circuit?
The earth’s surface has a negative surface charge density of 10−9 C m−2. The potential difference of 400 kV between the top of the atmosphere and the surface results (due to the low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmospheric electric field, how much time (roughly) would be required to neutralise the earth’s surface? (This never happens in practice because there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe). (Radius of earth = 6.37 × 106 m.)
Can the potential difference across a battery be greater than its emf?
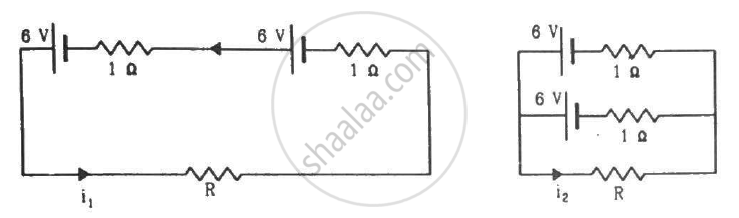
Find the value of i1/i2 in the following figure if (a) R = 0.1 Ω (b) R = 1 Ω and (c) R = 10 Ω. Note from your answers that in order to get more current from a combination of two batteries, they should be joined in parallel if the external resistance is small and in series if the external resistance is large, compared to the internal resistance.
A battery of emf 100 V and a resistor of resistance 10 kΩ are joined in series. This system is used as a source to supply current to an external resistance R. If R is not greater than 100 Ω, the current through it is constant up to two significant digits.
Find its value. This is the basic principle of a constant-current source.
How many time constants will elapse before the power delivered by a battery drops to half of its maximum value in an RC circuit?
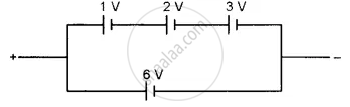
Find the emf of the battery shown in the figure:
Answer the following question.
What is the end error in a meter bridge? How is it overcome? The resistances in the two arms of the metre bridge are R = Ω and S respectively. When the resistance S is shunted with equal resistance, the new balance length found to be 1.5 l1, where l2 is the initial balancing length. calculate the value of s.

If n cells each of emf e and internal resistance r are connected in parallel, then the total emf and internal resistance will be ______.
