Advertisements
Advertisements
Question
“A uniformly charged conducting spherical shell for the points outside the shell behaves as if the entire charge of the shell is concentrated at its centre”. Show this with the help of a proper diagram and verify this statement.
Solution
A shell of radius R is carrying uniformly distributed charge of charge density σ.
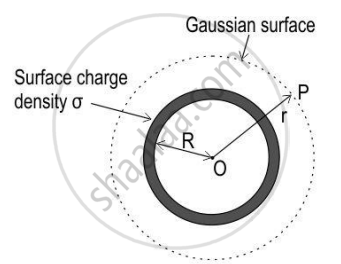
Electric field E at point P at a distance r from the centre of a uniformly charged spherical shell:
Consider a Gaussian surface to be a sphere of radius r >R and with centre O, passing through P.
Using the principles of spherical symmetry, E and area vector ΔS at every point are parallel, flux through each of the area element.
ΔΦ = E. ΔS
Summing over all ΔS,
Φ = E × 4 π R2
The charge enclosed is σ × 4 π R2
By Gauss’ law,
`"E" xx 4 pi "r"^2 = "q"/ε_o = (σ "X" 4pi "R"^2)/ε_o`
`"E" = (σ "R"^2)/(ε_o "r"^2) = "q"/(4 pi ε_o "r"^2)`
This formula is exactly similar to the field produced by a point charge q placed at the centre O, that is, as per Coulomb’s law.
APPEARS IN
RELATED QUESTIONS
Find the electric field intensity due to a uniformly charged spherical shell at a point (ii) inside the shell. Plot the graph of electric field with distance from the centre of the shell.
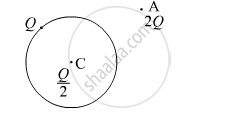
A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge`Q/2` is placed at its centre C and an other charge +2Q is placed outside the shell at a distance x from the centre as shown in the figure. Find (i) the force on the charge at the centre of shell and at the point A, (ii) the electric flux through the shell.
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 × 10−22 C/m2. What is E:
- in the outer region of the first plate,
- in the outer region of the second plate, and
- between the plates?
A small conducting sphere of radius 'r' carrying a charge +q is surrounded by a large concentric conducting shell of radius Ron which a charge +Q is placed. Using Gauss's law, derive the expressions for the electric field at a point 'x'
(i) between the sphere and the shell (r < x < R),
(ii) outside the spherical shell.
Using Gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
A charge Q is uniformly distributed on a spherical shell. What is the field at the centre of the shell? If a point charge is brought close to the shell, will the field at the centre change? Does your answer depend on whether the shell is conducting or non-conducting?
A positive point charge Q is brought near an isolated metal cube.
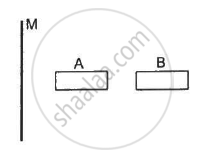
A large non-conducting sheet M is given a uniform charge density. Two uncharged small metal rods A and B are placed near the sheet as shown in the following figure.
(a) M attracts A.
(b) M attracts B.
(c) A attracts B.
(d) B attracts A.
Find the flux of the electric field through a spherical surface of radius R due to a charge of 10−7 C at the centre and another equal charge at a point 2R away from the centre in the following figure.