Advertisements
Advertisements
Question
The circumference of a circle is equal to the sum of the circumference of two circles having diameters 36 cm and 20 cm. The radius of the new circle is
Options
16 cm
28 cm
42 cm
56 cm
Solution
28 cm
Let r cm be the radius of the new circle.
We know:
Circumference of the new circle = Circumference of the circle with diameter 36 cm + Circumference of the circle with diameter 20 cm
Thus, we have:
2πr = 2πr + 2πr2
⇒ 2πr = (2π × 18) + (2π × 10)
⇒ 2πr = 2π × (18 + 10)
⇒ 2πr = (2πr × 28 )
`⇒ 2πr =( 2 × 22/7xx28)`
⇒ 2πr = 176
`⇒ 2 × 22/7xx"r"=176`
`=> "r" = (176xx7/44)`
⇒ r =28 cm
APPEARS IN
RELATED QUESTIONS
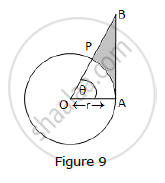
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
A car has wheels which are 80 cm in diameter. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour ?
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the costs of the rope, if it cost ₹ 4 per meter. (Take `pi = 22/7`)
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
The area of a circle is 49 π cm2. Its circumference is:
The diameter of a wheel is 84 cm. How many revolutions will it make to cover 792 m?
The area between the circumferences of two concentric circles is 2464 cm2. If the inner circle has circumference of 132 cm, calculate the radius of outer circle.
A 7 m road surrounds a circular garden whose area is 5544 m2. Find the area of the road and the cost of tarring it at the rate of Rs.150 per sq m.
The diameters of the front and the rear wheels of a tractor are 63 cm and 1.54 m respectively. The rear wheel is rotating at `24 6/11` revolutions per minute. Find:
(i) the revolutions per minute made by the front wheel.
(ii) the distance traveled bu the tractor in 40 minutes.
Find the circumference of the circles whose radii are given below.
49 cm
