Advertisements
Advertisements
Question
The cross-section of a canal is a trapezium in shape. If the canal is 10 m wide at the top 6 m wide at the bottom and the area of cross-section is 72 m2 determine its depth.
Solution
Let the depth of canal bed.
Given:
Lengths of the parallel sides of the trapezium shape canal are 10 m and 6 m.
And, the area of the cross section of the canal is 72 m2 .
Area of trapezium \[=\frac{1}{2}\times(\text{ Sum of the parallel sides })\times(\text{ Perpendicular distance between the parallel sides })\]
\[72 = \frac{1}{2} \times (10+6)\times(d)\]
\[72 = 8\times d\]
\[d =\frac{72}{8}= 9 m\]
APPEARS IN
RELATED QUESTIONS
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Find the altitude of a trapezium whose area is 65 cm2 and whose bases are 13 cm and 26 cm.
The area of a trapezium is 384 cm2. Its parallel sides are in the ratio 3 : 5 and the perpendicular distance between them is 12 cm. Find the length of each one of the parallel sides.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.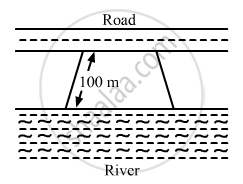
If the area of a trapezium is 28 cm2 and one of its parallel sides is 6 cm, find the other parallel side if its altitude is 4 cm.
The two parallel sides and the distance between them are in the ratio 3: 4: 2. If the area of the trapezium is 175 cm2, find its height.
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq.cm
The area of the trapezium, if the parallel sides are measuring 8 cm and 10 cm and the height 5 cm is
In a trapezium if the sum of the parallel sides is 10 cm and the area is 140 sq.cm, then the height is
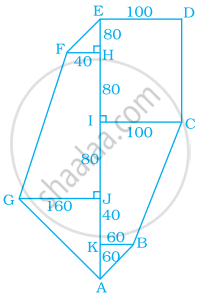
Find the area of the following fields. All dimensions are in metres.