Advertisements
Advertisements
Question
The curved surface area and the volume of a toy, cylindrical in shape, are 132 cm2 and 462 cm3 respectively. Find, its diameter and its length.
Solution
Let the radius of a toy = r and
height of the toy = h
The curved surface area of a toy = 132 cm2
=> 2πrh = 132 cm2
⇒ `2pirh = 132` cm2
⇒ `r = 132/(2pi xx h)` cm2 ...(i)
Also, volume of a toy = 462 cm3
⇒ `pir^2h = 462` cm3
⇒ `r^2 = 462/(pi xx h)` ...(ii)
Now, substitute the volume of r, we get
`(132)^2/((2)^2 xx (pi)^2 xx h^2) = 462/(pi xx h)`
⇒ `132^2/(4 xx pi xx h) = 462`
⇒ `4 xx pi xx h = (132 xx 132)/462`
⇒ `h = (132 xx 132)/(462 xx pi xx h)`
⇒ `h = (132 xx 132 xx 7)/(462 xx 22 xx 4) = 3` cm
Now, put the value of h in eq. (i), we get
`r = (132 xx 7)/(2 xx 22 xx 3) = 7` cm
∴ Diameter of the toy = `2 xx r`
= `2 xx 7` cm = 14 cm
- Diameter: 14 cm
- Length (Height): 3 cm
APPEARS IN
RELATED QUESTIONS
The paint in a certain container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
 |
 |
| (a) | (b) |
The length of a hall is 18 m and the width 12 m. The sum of the areas of the floor and the
flat roof is equal to the sum of the areas of the four walls. Find the height of the hall.
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost ofcovering it with sheet of paper at the rates of Rs. 8 and Rs. 9.50 per m2 is Rs.1248. Find the dimensions of the box.
An open box is made of wood 3 cm thick. Its external length, breadth and height are 1.48 m, 1.16 m and 8.3 m. Find the cost of painting the inner surface of Rs 50 per sq. metre.
Find the volume of a cuboid whose length = 12 cm, breadth = 8 cm, height = 6 cm.
A milk container is 8 cm long and 50 cm wide. What should be its height so that it can hold 4 litres of milk?
Find the number of cuboidal boxes measuring 2 cm by 3 cm by 10 cm which can be stored in a carton whose dimensions are 40 cm, 36 cm and 24 cm.
How much clay is dug out in digging a well measuring 3 m by 2 m by 5 m?
A swimming pool is 250 m long and 130 m wide. 3250 cubic metres of water is pumped into it. Find the rise in the level of water.
Find the surface area of a cuboid whose llength = 2 m, breadth = 4 m, height = 5 m .
A cloassroom is 11 m long, 8 m wide and 5 m high. Find the sum of the areas of its floor and the four walls (including doors, windows, etc.)
Show that the product of the areas of the floor and two adjacent walls of a cuboid is the square of its volume.
The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5 m, 3 m and 350 cm, respectively. Find the cost of plastering at the rate of Rs 8 per square metre.
The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu. dm. Find its dimensions.
A field is 150 m long and 100 m wide. A plot (outside the field) 50 m long and 30 m wide is dug to a depth of 8 m and the earth taken out from the plot is spread evenly in the field. By how much is the level of field raised?
Three cubes of metal whose edges are in the ratio 3 : 4 : 5 are melted down in to a single cube whose diagonal is 12 `sqrt(3)` cm. Find the edges of three cubes.
If each edge of a cuboid of surface area S is doubled, then surface area of the new cuboid is
The external dimensions of a closed wooden box are 27 cm, 19 cm, and 11 cm. If the thickness of the wood in the box is 1.5 cm; find:
- The volume of the wood in the box;
- The cost of the box, if wood costs Rs. 1.20 per cm3;
- A number of 4 cm cubes that could be placed into the box.
The internal length, breadth, and height of a closed box are 1 m, 80 cm, and 25 cm. respectively. If its sides are made of 2.5 cm thick wood; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
The height of a circular cylinder is 20 cm and the diameter of its base is 14 cm. Find:
(i) the volume
(ii) the total surface area.
In a building, there are 24 cylindrical pillars. For each pillar, the radius is 28 m, and the height is 4 m. Find the total cost of painting the curved surface area of the pillars at the rate of ₹ 8 per m2.
If the edge of a cube is 8 cm long, find its total surface area.
The dimensions of a cuboidal box are 6 m × 400 cm × 1.5 m. Find the cost of painting its entire outer surface at the rate of ₹ 22 per m2.
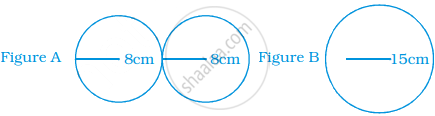
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?