Advertisements
Advertisements
Question
The length of a hall is 18 m and the width 12 m. The sum of the areas of the floor and the
flat roof is equal to the sum of the areas of the four walls. Find the height of the hall.
Solution
Length of the hall = 18m
Width of hall = 12m
Now given,
Area of the floor and the flat roof = sum of the areas of four walls.
`⇒2lb=2lh+2bh`
`⇒lb= lh+bh`
`⇒h=(lb)/(l+b)=(18xx12)/(18+12)=(216)/30`
`=7.2m`
APPEARS IN
RELATED QUESTIONS
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
 |
 |
| (a) | (b) |
The length and breadth of a hall are in the ratio 4: 3 and its height is 5.5 metres. The cost of decorating its walls (including doors and windows) at Rs. 6.60 per square metre is Rs. 5082. Find the length and breadth of the room.
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm in following figure. The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2. Find the total expenses required for polishing and painting the surface of the bookshelf.

Find the volume of a cuboid whose length =1.2 m, breadth = 30 cm, height = 15 cm.
Find the height of a cuboid of volume 100 cm3, whose length and breadth are 5 cm and 4 cm respectively.
Find the weight of solid rectangular iron piece of size 50 cm × 40 cm × 10cm, if 1 cm3 of iron weighs 8 gm.
Find the number of cuboidal boxes measuring 2 cm by 3 cm by 10 cm which can be stored in a carton whose dimensions are 40 cm, 36 cm and 24 cm.
Find the area of the cardboard required to make a closed box of length 25 cm, 0.5 m and height 15 cm.
The internal length, breadth, and height of a closed box are 1 m, 80 cm, and 25 cm. respectively. If its sides are made of 2.5 cm thick wood; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
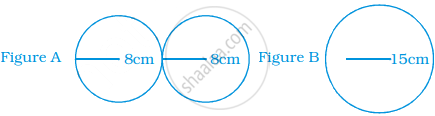
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?