Advertisements
Advertisements
Question
The dining-hall of a hotel is 75 m long; 60 m broad and 16 m high. It has five – doors 4 m by 3 m each and four windows 3 m by 1.6 m each. Find the cost of :
(i) papering its walls at the rate of Rs.12 per m2;
(ii) carpetting its floor at the rate of Rs.25 per m2.
Solution
Length of the dining hall of a hotel = 75 m
The breadth of the dining hall of a hotel = 60 m
Height of the dining hall of a hotel = 16 m
(i) Area of four walls of the dining hall = 2[L+B) x H = 2(75 + 60) x 16
= `2(135) xx 16`
= `270 xx 16`
= 4320 m2
Area of one door = `4 xx 3` m2
= 12 m2
Area of 5 doors = `12 xx 5 = 60` m2
Area of one window = `3 xx 1.6 = 4.8`m2
Area of 4 window = `4.8 xx 4 = 19.2`m2
Area of the walls to be papered
= 4320 - (60 + 19.2)
= 4320 - 79.2
= 4240.8 m2
Cost of papering the walls @ Rs.12 per m2
= `4240.8 xx 12`
= Rs. 50889.60
(ii) Area of floor = L × B
= `75 xx 60`
= 4500 m2
Cost of carpetting the floor @ Rs. 25 per m2
= 4500 × 25
= Rs. 112500
APPEARS IN
RELATED QUESTIONS
The paint in a certain container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
 |
 |
| (a) | (b) |
Water is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of the reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
Find the lateral surface area and total surface area of a cube of edge 10 cm.
An open box is made of wood 3 cm thick. Its external length, breadth and height are 1.48 m, 1.16 m and 8.3 m. Find the cost of painting the inner surface of Rs 50 per sq. metre.
The paint in a certain container is sufficient to paint on area equal to 9.375 m2. How manybricks of dimension 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
Find the number of cuboidal boxes measuring 2 cm by 3 cm by 10 cm which can be stored in a carton whose dimensions are 40 cm, 36 cm and 24 cm.
A cuboidal block of solid iron has dimensions 50 cm, 45 cm and 34 cm. How many cuboids of size 5 cm by 3 cm by 2 cm can be obtained from this block? Assume cutting causes no wastage.
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions is length = 12 m, breadth = 10 m, height = 4.5 cm.
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions islength = 4 m, breadth = 2.5 m, height = 50 cm.
How many planks each of which is 3 m long, 15 cm broad and 5 cm thick can be prepared from a wooden block 6 m long, 75 cm broad and 45 cm thick?
A swimming pool is 250 m long and 130 m wide. 3250 cubic metres of water is pumped into it. Find the rise in the level of water.
The length, width and height of a rectangular solid are in the ratio of 3 : 2 : 1. If the volume of the box is 48cm3, the total surface area of the box is
If each edge of a cube, of volume V, is doubled, then the volume of the new cube is
The cost of constructing a wall 8 m long, 4 m high and 10 cm thick at the rate of Rs. 25 per m3 is
If A1, A2, and A3 denote the areas of three adjacent faces of a cuboid, then its volume is
The length, breadth, and height of a cuboid are in the ratio 5 : 3: 2. If its volume is 240 cm3; find its dimensions. Also, find the total surface area of the cuboid.
Find the length of each edge of a cube, if its volume is :
(i) 216 cm3
(ii) 1.728 m3
The internal length, breadth, and height of a closed box are 1 m, 80 cm, and 25 cm. respectively. If its sides are made of 2.5 cm thick wood; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
A cube of edge 6 cm and a cuboid with dimensions 4 cm x x cm x 15 cm are equal in volume. Find:
(i) the value of x.
(ii) the total surface area of the cuboid.
(iii) the total surface area of the cube.
(iv) which of these two has a greater surface and by how much?
A cylindrical pillar has a radius of 21 cm and a height of 4 m. Find:
- The curved surface area of the pillar.
- cost of polishing 36 such cylindrical pillars at the rate of ₹12 per m2.
If radii of two cylinders are in the ratio 4 : 3 and their heights are in the ratio 5: 6, find the ratio of their curved surfaces.
A closed box is made of wood 5 mm thick. The external length, breadth and height of the box are 21 cm, 13 cm and 11 cm respectively. Find the volume of the wood used in making the box.
A room is 5m long, 2m broad and 4m high. Calculate the number of persons it can accommodate if each person needs 0.16m3 of air.
Find the volume of wood used in making a closed box 22 cm by 18 cm by 14 cm, using a 1 cm thick wood. Also, find the cost of wood required to make the box at the rate of Rs. 5 per cm³ How many cubes of side 2 cm can be placed in the box?
Three identical cubes of side 4 cm are joined end to end. Find the total surface area and lateral surface area of the new resulting cuboid
Opposite faces of a cuboid are ______ in area.
The areas of any two faces of a cuboid are equal.
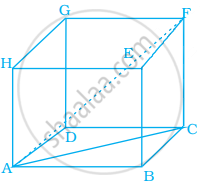
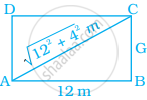
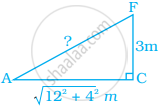
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.