Advertisements
Advertisements
Question
The equation of the circle circumscribing the triangle whose sides are the lines y = x + 2, 3y = 4x, 2y = 3x is ______.
Solution
The equation of the circle circumscribing the triangle whose sides are the lines y = x + 2, 3y = 4x, 2y = 3x is x2 + y2 – 46x + 22y = 0
Explanation: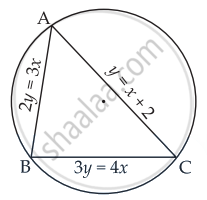
Let AB represents 2y = 3x ......(i)
BC represents 3y = 4x ......(ii)
And AC represents y = x + 2 .......(iii)
From equation (i) and (ii)
2y = 3x
⇒ y = `(3x)/2`
Putting the value of y in equation (ii) we get
`3((3x)/2) = 4x`
⇒ 9x = 8x
⇒ x = 0 and y = 0
From equation (i) and (iii) we get
y = x + 2
Putting y = x + 2 in equation (i) we get
2(x + 2) = 3x
⇒ 2x + 4 = 3x
⇒ x = 4 and y = 6
∴ Coordinates of B = (0, 0)
From equation (i) and (iii) we get
y = x + 2
Putting y = x + 2 in equation (i) we get
2(x + 2) = 3x
⇒ 2x + 4 = 3x
⇒ x = 4 and y = 6
∴ Coordinates of A = (4, 6)
Solving equation (ii) and (iii) we get
y = x + 2
Putting the value of y in equation (ii) we get
3(x + 2) = 4x
⇒ 3x + 6 = 4x
⇒ x = 6 and y = 8
∴ Coordinates of C = (6, 8)
It implies that the circle is passing through (0, 0), (4, 6) and (6, 8).
We know that the general equation of the circle is
x2 + y2 + 2gx + 2fy + c = 0 ......(i)
Since the points (0, 0), (4, 6) and (6, 8) lie on the circle then
0 + 0 + 0 + 0 + c = 0
⇒ c = 0
16 + 36 + 8g + 12f + c = 0
⇒ 8g + 12f + 0 = – 52
⇒ 2g + 3f = – 13 ......(ii)
And 36 + 64 + 12g + 16f + c = 0
⇒ 12g + 16f + 0 = – 100
⇒ 3g + 4f = – 25 .......(iii)
Solving equation (ii) and (iii) we get
2g + 3f = – 13
3g + 4f = – 25
⇒ 6g + 9f = – 39
6g + 8f = – 50
(–) (–) (+)
f = 11
Putting the value of f in equation (ii) we get
2g + 3 × 11 = – 13
⇒ 2g + 33 = – 13
⇒ 2g = – 46
⇒ g = – 23
Putting the values of g, f and c in equation (i) we get
x2 + y2 + 2(– 23)x + 2(11)y + 0 = 0
⇒ x2 + y2 – 46x + 22y = 0
APPEARS IN
RELATED QUESTIONS
Find the equation of the circle with:
Centre (a cos α, a sin α) and radius a.
Find the equation of the circle whose centre is (1, 2) and which passes through the point (4, 6).
Find the equation of the circle passing through the point of intersection of the lines x + 3y = 0 and 2x − 7y = 0 and whose centre is the point of intersection of the lines x + y + 1 = 0 and x − 2y + 4 = 0.
A circle whose centre is the point of intersection of the lines 2x − 3y + 4 = 0 and 3x + 4y− 5 = 0 passes through the origin. Find its equation.
If the lines 3x − 4y + 4 = 0 and 6x − 8y − 7 = 0 are tangents to a circle, then find the radius of the circle.
Find the coordinates of the centre and radius of each of the following circles: 2x2 + 2y2 − 3x + 5y = 7
Find the coordinates of the centre and radius of each of the following circles: x2 + y2 − ax − by = 0
Find the equation of the circle passing through the points:
(0, 0), (−2, 1) and (−3, 2)
Find the equation of the circle which passes through the points (3, 7), (5, 5) and has its centre on the line x − 4y = 1.
Find the equation of the circle which circumscribes the triangle formed by the lines
x + y = 2, 3x − 4y = 6 and x − y = 0.
Find the equation of the circle which circumscribes the triangle formed by the lines y = x + 2, 3y = 4x and 2y = 3x.
Find the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the positive side of the x-axis and y-axis respectively.
Find the equation of the circle concentric with x2 + y2 − 4x − 6y − 3 = 0 and which touches the y-axis.
If a circle passes through the point (0, 0),(a, 0),(0, b) then find the coordinates of its centre.
Find the equation of the circle which passes through the origin and cuts off intercepts aand b respectively from x and y - axes.
Find the equation of the circle whose diameter is the line segment joining (−4, 3) and (12, −1). Find also the intercept made by it on y-axis.
The line 2x − y + 6 = 0 meets the circle x2 + y2 − 2y − 9 = 0 at A and B. Find the equation of the circle on AB as diameter.
Find the equation of the circle which circumscribes the triangle formed by the lines x = 0, y = 0 and lx + my = 1.
Find the equations of the circles which pass through the origin and cut off equal chords of \[\sqrt{2}\] units from the lines y = x and y = − x.
Write the coordinates of the centre of the circle passing through (0, 0), (4, 0) and (0, −6).
If the abscissae and ordinates of two points P and Q are roots of the equations x2 + 2ax − b2 = 0 and x2 + 2px − q2 = 0 respectively, then write the equation of the circle with PQ as diameter.
Write the area of the circle passing through (−2, 6) and having its centre at (1, 2).
If 2x2 + λxy + 2y2 + (λ − 4) x + 6y − 5 = 0 is the equation of a circle, then its radius is
If the centroid of an equilateral triangle is (1, 1) and its one vertex is (−1, 2), then the equation of its circumcircle is
The equation of the circle passing through the origin which cuts off intercept of length 6 and 8 from the axes is
