Question

An ellipse is described by using an endless string which is passed over two pins. If the axes are 6 cm and 4 cm, the length of the string and distance between the pins are ______.

Answer 1

An ellipse is described by using an endless string which is passed over two pins. If the axes are 6 cm and 4 cm, the length of the string and distance between the pins are `6 + 2sqrt(5)` cm and `2sqrt(5)` cm.

Explanation:

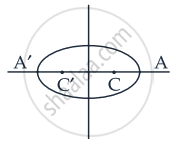
Let equation of ellipse is `x^2/a^2 + y^2/b^2` = 1

Here 2a = 6 ⇒ a = 3

And 2b = 4 ⇒ b = 2

We know that c² = a² – b²

= (3)² – (2)²

= 9 – 4

= 5

c = `sqrt(5)`

We have e = `c/a`

⇒ e = `sqrt(5)/3`

Length of string = 2a + 2ae = 2a(1 + e)

= `6(1 + sqrt(5)/3)`

= `(6(3 + sqrt(5)))/3`

= `6 + 2sqrt(5)`

Distance between the pins = CC'

= 2ae

= `2 xx 3 xx sqrt(5)/3`

= `2sqrt(5)`