Advertisements
Advertisements
Question
The figure shows the cross section of 0.2 m a concrete wall to be constructed. It is 0.2 m wide at the top, 2.0 m wide at the bottom and its height is 4.0 m, and its length is 40 m. Calculate the volume of the concrete in the wall
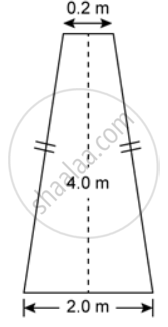
Solution
Area of the cross section of the wall
= 4.4 sq.m ....from (a)
Volume of the wall
= Area of the cross section x length
= 4.4 x 40
= 176m3
∴ Volume of the wall is 176m3.
APPEARS IN
RELATED QUESTIONS
The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimeters.
Assume that all angles in the figures are right angles.
The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimeters.
Assume that all angles in the figures are right angles.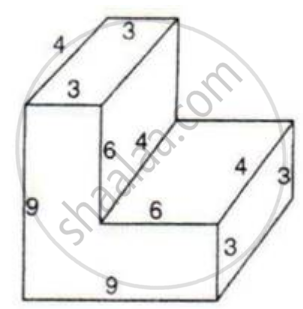
A swimming pool is 40 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 3 m deep respectively. If the bottom of the pool slopes uniformly, find the amount of water in liters required to fill the pool.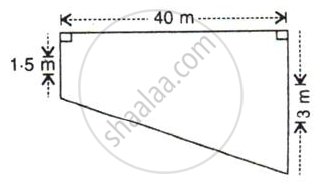
The following figure shows a closed victory-stand whose dimensions are given in cm.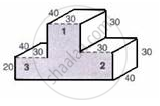
Find the volume and the surface area of the victory stand.
A school auditorium is 40 m long, 30 m broad and 12 m high. If each student requires 1.2 m2 of the floor area; find the maximum number of students that can be accommodated in this auditorium. Also, find the volume of air available in the auditorium, for each student.
The internal dimensions of a rectangular box are 12 cm x `x` cm x 9 cm. If the length of the longest rod that can be placed in this box is 17 cm; find `x`.
A rectangular field is 112 m long and 62 m broad. A cubical tank of edge 6 m is dug at each of the four corners of the field and the earth so removed is evenly spread on the remaining field. Find the rise in level.
Find the length of 22 kg copper wire of diameter 0.8 cm, if the weight of 1 cm3 copper is 4.2 g.
The figure represents the cross section of a swimming pool 10 m broad, 2 m deep at one end, 3 m deep at the other end. Calculate the volume of water it will hold when full, given that its length is 40 m.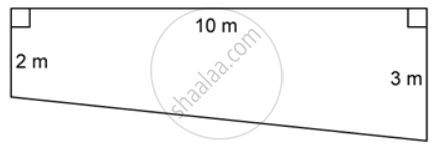
ABCDE is the end view of a factory shed which is 50 m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.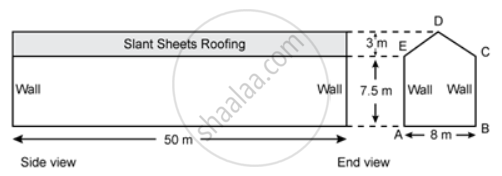
Calculate the total volume content of the shed.
