Advertisements
Advertisements
Question
The following figure shows a closed victory-stand whose dimensions are given in cm.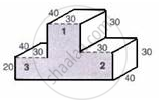
Find the volume and the surface area of the victory stand.
Advertisements
Solution
Consider the box 1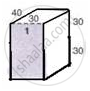
Thus, the dimensions of box 1 are 60 cm, 40 cm, and 30 cm.
Therefore, the volume of box 1 = 60 x 40 x 30 = 72000 cm3
Surface area of box 1 = 2 ( lb + bh + lh )
Since the box is open at the bottom and from the given figure, we have,
Surface area of box 1 = 40 x 40 + 40 x 30 + 40 x 30 + 2 ( 60 x 30 )
= 1600 + 1200 + 1200 + 3600
= 7600 cm2
Consider the box 2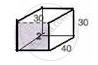 
Thus, the dimensions of box 2 are 40 cm, 30 cm, and 30 cm.
Therefore, the volume of box 2 = 40 x 30 x 30 = 36000 cm3
Surface area of box 2 = 2 ( lb + bh + lh )
Since the box is open at the bottom and from the given figure, we have,
Surface area of box 2 = 40 x 30 + 40 x 30 + 2 ( 30 x 30 )
= 1200 + 1200 + 1800
= 4200 cm2
Consider the box 3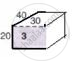
Thus, the dimensions of the box 3 are 40 cm, 30 cm, and 20 cm.
Therefore, the volume of box 3 = 40 x 30 x 20 = 24000 cm3
Surface area of box 3 = 2 ( lb + bh + lh )
Since the box is open at the bottom and from the given figure, we have,
Surface area of box 3 = 40 x 30 + 40 x 20 + 2 ( 30 x 20 )
= 1200 + 800 + 1200
= 3200 cm2
Total volume of the box
= volume of box 1 + volume of box 2 + volume of box 3
= 72000 + 36000 + 24000
= 132000 cm3
Similarly, total surface area of the box
= surface area of box 1 + surface area of box 2 + surface area of box 3
= 7600 + 4200 + 3200
= 15000 cm2
APPEARS IN
RELATED QUESTIONS
A swimming pool is 40 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 3 m deep respectively. If the bottom of the pool slopes uniformly, find the amount of water in liters required to fill the pool.
A swimming pool is 18 m long and 8 m wide. Its deep and shallow ends are 2 m and 1.2 m respectively. Find the capacity of the pool, assuming that the bottom of the pool slopes uniformly.
A rectangular cardboard sheet has length 32 cm and breadth 26 cm. Squares each of side 3 cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.
The cross section of a piece of metal 2 m in length
is shown. Calculate the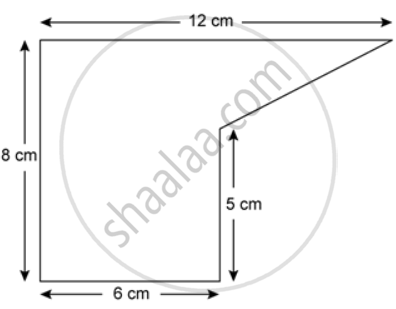 volume of the piece of metal.
The given figure is a cross -section of a victory stand used in sports. All measurements are in centimetres. Assume all angles in the figure are right angles. If the width of the stand is 60 cm, find The space it occupies in cm3.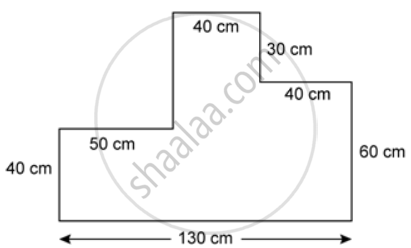
A swimming pool is 50 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 4.5 m respectively. If the bottom of the pool slopes uniformly, find the amount of water in kilolitres required to fill the pool (1 m3 = 1000 liters).
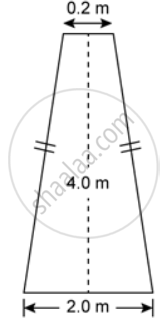
The figure shows the cross section of 0.2 m a concrete wall to be constructed. It is 0.2 m wide at the top, 2.0 m wide at the bottom and its height is 4.0 m, and its length is 40 m. Calculate the volume of the concrete in the wall
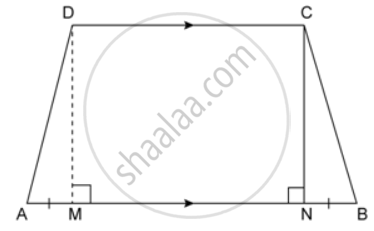
The cross section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN; AB = 4.4 m, CD = 3 m The height of a tunnel is 2.4 m. The tunnel is 5.4 m long. Calculate the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per m2.
ABCDE is the end view of a factory shed which is 50 m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.
Calculate the total volume content of the shed.
ABCDE is the end view of a factory shed which is 50 m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.
If the cost of asbestos sheet roofing is Rs. 20 per m2, find the cost of roofing.
