Advertisements
Advertisements
Question
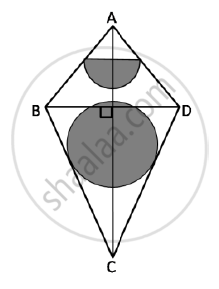
The given figure represents a kite with a circular and a semicircular motifs stuck on it.
The radius of a circle is 2.5 cm and the semicircle is 2 cm. If diagonals AC and BD are
of lengths 12 cm and 8 cm respectively, find the area of the:
1) Shaded part. Give your answer correct to the nearest whole number.
2) Unshaded part
Solution
1) Area of the shaded part = Area of the circle + area of the semicircle
`= pi(2.5)^2 + (pi(2)^2)/2`
`= pi[6.25+2]`
`= 22/7 [8.25]`
`~~ 26 cm^2`
2) Area of kite = `"product of the diagonals"/2` = `(AC xx BD)/2 = (12xx8)/2 = 48 cm^2`
Area of the unshaded part = Area of the kite - Area of the shaded part
= 48 - 26
= `22 cm^2`
APPEARS IN
RELATED QUESTIONS
In the given figure ABCD is a rectangle. It consists of a circle and two semi-circles each of
which are of radius 5 cm. Find the area of the shaded region. Give your answer correct to
three significant figures

Use graph paper for this question (Take 2 cm = 1 unit along both x and y-axis). ABCD is a quadrilateral whose vertices are A(2, 2), B(2, –2), C(0, –1) and D(0, 1).
1) Reflect quadrilateral ABCD on the y-axis and name it as A'B'CD
2) Write down the coordinates of A' and B'.
3) Name two points which are invariant under the above reflection
4) Name the polygon A'B'CD
Three vertices of parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2)
1) the coordinate of the fourth vertex D
2) length of diagonal BD
3) equation of the side AD of the parallelogram ABCD
Using a graph paper, plot the points A(6, 4) and B(0, 4).
- Reflect A and B in the origin to get the images A' and B'.
- Write the co-ordinates of A' and B'.
- State the geometrical name for the figure ABA'B'.
- Find its perimeter.
Show that A(3, 2), B(6, −2) and C(2, −5) can be the vertices of a square.
- Find the co-ordinates of its fourth vertex D, if ABCD is a square.
- Without using the co-ordinates of vertex D, find the equation of side AD of the square and also the equation of diagonal BD.
P(3, 4), Q(7, –2) and R(–2, –1) are the vertices of triangle PQR. Write down the equation of the median of the triangle through R.
A line AB meets the x-axis at point A and y-axis at point B. The point P(−4, −2) divides the line segment AB internally such that AP : PB = 1 : 2. Find:
- the co-ordinates of A and B.
- equation of line through P and perpendicular to AB.
Point A and B have co-ordinates (7, −3) and (1, 9) respectively. Find:
- the slope of AB.
- the equation of perpendicular bisector of the line segment AB.
- the value of ‘p’ of (−2, p) lies on it.
A line is of length 10 units and one end is at the point (2, – 3). If the abscissa of the other end be 10, prove that its ordinate must be 3 or – 9.
