Advertisements
Advertisements
Question
Using a graph paper, plot the points A(6, 4) and B(0, 4).
- Reflect A and B in the origin to get the images A' and B'.
- Write the co-ordinates of A' and B'.
- State the geometrical name for the figure ABA'B'.
- Find its perimeter.
Solution
a.

b. Co-ordinates of A' = (–6, –4)
Co-ordinates of B' = (0, –4)
c. ABA'B' is a parallelogram.
d. In ΔBA'B', BB' = 8 units, A'B' = 6 units
∴ BA' = `sqrt(6^2 + 8^2)`
= `sqrt(36 + 64)`
= `sqrt(100)`
= 10 units
`\implies` B'A = 10 units
AB = A'B' = 6 units
Perimeter of ABA'B'
= AB + BA' + A'B' + B'A
= 6 + 10 + 6 + 10
= 32 units
APPEARS IN
RELATED QUESTIONS
In the given figure ABCD is a rectangle. It consists of a circle and two semi-circles each of
which are of radius 5 cm. Find the area of the shaded region. Give your answer correct to
three significant figures

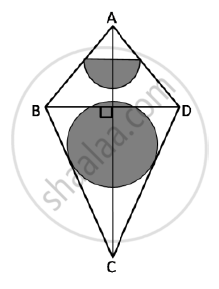
The given figure represents a kite with a circular and a semicircular motifs stuck on it.
The radius of a circle is 2.5 cm and the semicircle is 2 cm. If diagonals AC and BD are
of lengths 12 cm and 8 cm respectively, find the area of the:
1) Shaded part. Give your answer correct to the nearest whole number.
2) Unshaded part
Use graph paper for this question (Take 2 cm = 1 unit along both x and y-axis). ABCD is a quadrilateral whose vertices are A(2, 2), B(2, –2), C(0, –1) and D(0, 1).
1) Reflect quadrilateral ABCD on the y-axis and name it as A'B'CD
2) Write down the coordinates of A' and B'.
3) Name two points which are invariant under the above reflection
4) Name the polygon A'B'CD
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects the co-ordinate axes at points A and B. M is the mid-point of the segment AB. Find:
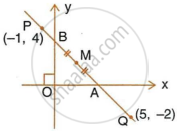
- The equation of the line.
- The co-ordinates of A and B.
- The co-ordinates of M.
Show that A(3, 2), B(6, −2) and C(2, −5) can be the vertices of a square.
- Find the co-ordinates of its fourth vertex D, if ABCD is a square.
- Without using the co-ordinates of vertex D, find the equation of side AD of the square and also the equation of diagonal BD.
O(0, 0), A(3, 5) and B(−5, −3) are the vertices of triangle OAB. Find the equation of median of triangle OAB through vertex O.
P(3, 4), Q(7, –2) and R(–2, –1) are the vertices of triangle PQR. Write down the equation of the median of the triangle through R.
A line AB meets the x-axis at point A and y-axis at point B. The point P(−4, −2) divides the line segment AB internally such that AP : PB = 1 : 2. Find:
- the co-ordinates of A and B.
- equation of line through P and perpendicular to AB.
Use a graph sheet for this question, take 2 cm = 1 unit along both x and y-axis:
- Plot the points A (3, 2) and B (5, 0). Reflect point A on the y-axis to A΄. Write co-ordinates of A΄.
- Reflect point B on the line AA΄ to B΄. Write the co-ordinates of B΄.
- Name the closed figure A’B’AB.
