Advertisements
Advertisements
Question
The hypotenuse of a right angled triangle is 25 cm and its perimeter 56 cm. Find the length of the smallest side
Solution
Perimeter of a right angle triangle = 56cm
Sum of the two sides + hypotenuse = 56
Sum of the two sides = 56 – 25
= 31 cm
Let one side of the triangle be “x”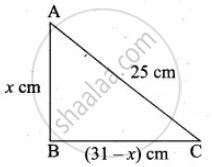
The other side of the triangle = (31 – x)cm
By Pythagoras theorem
AB2 + BC2 = AC2
x2 + (31 – x)2 = 252
x2 + 961 + x2 – 62x = 625
2x2 – 62x + 961 – 625 = 0
2x2 – 62x + 336 = 0
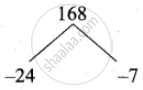
⇒ x2 – 31x + 168 = 0
(x – 24) (x – 7) = 0
x – 24 = 0 (or) x – 7 = 0
x = 24 (or) x = 7
Length of the smallest side is 7 cm
APPEARS IN
RELATED QUESTIONS
Solve the following quadratic equation by formula method
2x2 – 5x + 2 = 0
Solve the following quadratic equation by formula method
36y2 – 12ay + (a2 – b2) = 0
If the difference between a number and its reciprocal is `24/5`, find the number
A garden measuring 12m by 16m is to have a pedestrian pathway that is ‘ω’ meters wide installed all the way around so that it increases the total area to 285 m2. What is the width of the pathway?
From a group of 2x2 black bees, square root of half of the group went to a tree. Again eight-ninth of the bees went to the same tree. The remaining two got caught up in a fragrant lotus. How many bees were there in total?
Find the value of ‘k’ to identify the roots of the following equation is real and equal
(5k – 6)x2 + 2kx + 1 = 0
Find the value of ‘k’ to identify the roots of the following equation is real and equal
kx2 + (6k + 2)x + 16 = 0
Write the following expression in terms of α + β and αβ
`1/(alpha^2beta) + 1/(beta^2alpha)`
Write the following expression in terms of α + β and αβ
`(alpha + 3)/beta + (beta + 3)/alpha`
The roots of the equation x2 + 6x – 4 = 0 are α, β. Find the quadratic equation whose roots are α2β and β2α
