Question

There is a square field whose side is 10 m. A square flower bed is prepared in its centre leaving a gravel path all round the flower bed. The total cost of laying the flower bed and gravelling the path at ₹ 3 and ₹ 4 per square metre respectively is ₹ 364. Find the width of the gravel path

Answer 1

Let the width of the gravel path be ‘x’

Side of the flower bed = 10 – (x + x)

= 10 – 2x

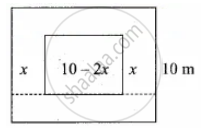
Area of the path way = Area of the field – Area of the flower bed

= 10 × 10 – (10 – 2x) (10 – 2x)sq.m

= 100 – (100 + 4x² – 40x)

= 100 – 100 – 4x² + 40x

= 40x – 4x² sq.m

Area of the flower bed = (10 – 2x) (10 – 2x)sq.m.

= 100 + 4x² – 40x

By the given condition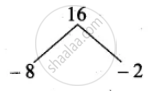

3(100 + 4x² – 40x) + 4(40x – 4x²) = 364

300 + 12x² – 120x + 160x – 16x² = 364

– 4x² + 40x + 300 – 364 = 0

– 4x² + 40x – 64 = 0   

⇒ x² – 10x + 16 = 0  ...(÷ by 4)

[The width must not be equal to 8 m since the side of the field is 10m]

(x – 8) (x – 2) = 0

x – 8 = 0 or x – 2 = 0

x = 8 or x = 2

Width of the gravel path = 2 m