Advertisements
Advertisements
Question
The radius of curvature of a convex mirror is 40 cm. Find its focal length.
Solution
Focal length = ½ (Radius of curvature)
Or, f =
APPEARS IN
RELATED QUESTIONS
Explain the following term related to spherical lenses:- optical centre
A diverging lens is used in:
(a) a magnifying glass
(b) a car to see objects on rear side
(c) spectacles for the correction of short sight
(d) a simple camera
If a spherical mirror breaks, what type of mirrors are the individual pieces?
Why does a driver use a convex mirror instead of a plane mirror as a rear view mirror?
Illustrate your answer with the help of a ray diagram.
Draw a ray diagram in each of the following cases to show the formation of image, when the object is placed :
(i) between the optical centre and principal focus of a convex lens.
(ii) anywhere in front of a concave lens.
(iii) at 2F of a convex lens.
State the signs and values of magnifications in the above-mentioned cases (i) and (ii).
An object 5 cm high forms a virtual image of 1.25 cm high, when placed in front of a convex mirror at a distance of 24 cm. Calculate:
- the position of the image
- the focal length of the convex mirror.
Define the term Centre of curvature.
Complete the following diagrams shown in the following figures by drawing the reflected rays.

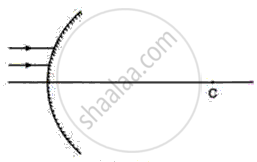
The diagram below shows the parallel rays incident on a convex mirror. C is the centre of the curvature of the mirror. By drawing the paths of the reflected rays, label the focus F and hence find the focal length of the mirror.
If the focal length of a spherical mirror is 10 cm, what is the value of its radius of curvature?
