Advertisements
Advertisements
Question
Three thin prisms are combined as shown in figure. The refractive indices of the crown glass for red, yellow and violet rays are μr, μy and μv respectively and those for the flint glass are μ'r, μ'y and μ'v respectively. Find the ratio A'/A for which (a) there is no net angular dispersion, and (b) there is no net deviation in the yellow ray.
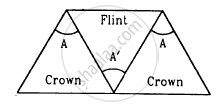
Solution
For the crown glass, we have:-
Refractive index for red rays = μr
Refractive index for yellow rays = μy
Refractive index for violet rays = μv
For the flint glass, we have:-
Refractive index for red rays = μ'r
Refractive index for yellow rays = μ'y
Refractive index for violet rays = μ'v
Let δcy and δfy be the angles of deviation produced by the crown and flint prisms for the yellow light.
Total deviation produced by the prism combination for yellow rays:-
δy = δcy − δfy
= 2δcy − δfy
=2(μcy + 1)A − (μfy − 1)A'
Angular dispersion produced by the combination is given by
δv − δr = [(μvc − 1)A − (μvf − 1)A' + (μvc − 1)A] − \[\left[ \left( \mu_{rc} - 1 \right)A - \left( \mu_{rf} - 1 \right)A' + \left( \mu_{rc} - 1 \right)A \right]\]
Here,
μvc = Refractive index for the violet colour of the crown glass
μvf = Refractive index for the violet colour of the flint glass
\[\mu_{rc}\] = Refractive index for the red colour of the crown glass
\[\mu_{rf}\] = Refractive index for the red colour of the flint glass
On solving, we get
δv − δr = 2(μvc −1)A − (μvf − 1)A'
(a) For zero angular dispersion, we have:
δt − δt = 0 = 2(μvc −1)A − (μvf − 1)A'
\[\Rightarrow \frac{A'}{A} = \frac{2( \mu_{vf} - 1)}{( \mu_{vc} - 1)}\]
\[ = \frac{2( \mu_r - \mu_r )}{( \mu_r - \mu)}\]
(b) For zero deviation in the yellow ray, δy = 0.
⇒ 2(μcy − 1)A = (μfy − 1)A
\[\Rightarrow \frac{A'}{A} = \frac{2( \mu_{cy} - 1)}{( \mu_{fy} - 1)}\]
\[ = \frac{2( \mu_y - 1)}{(\mu '_y - 1)}\]
APPEARS IN
RELATED QUESTIONS
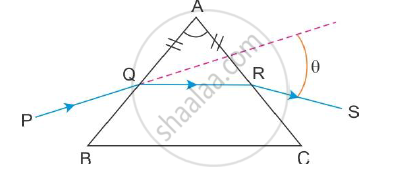
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60° and refractive index of material of prism is `sqrt3 `. Calculate angle θ.
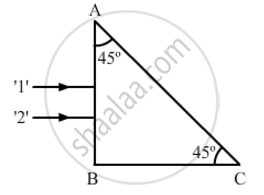
Two monochromatic rays of light are incident normally on the face AB of an isosceles right-angled prism ABC. The refractive indices of the glass prism for the two rays '1' and '2' are respectively 1.38 and 1.52. Trace the path of these rays after entering through the prism.
What is the cause of dispersion of light
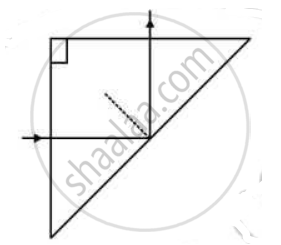
A ray of light incident normally on one face of a right isosceles prism is totally reflected, as shown in fig. What must be the minimum value of refractive index of glass? Give relevant calculations.
State any two difference between the primary rainbow and secondary rainbow
Draw the ray diagram showing refraction of light through a glass prism and hence obtain the relation between the refractive index μ of the prism, angle of prism and angle of minimum deviation.
Out of blue and red light which is deviated more by a prism? Give reason.
Can the dispersive power \[\omega = \frac{\mu_u - \mu_r}{\mu - 1}\] be negative? What is the sign of ω if a hollow prism is immersed into water?
The angular dispersion produced by a prism ___________ .
By properly combining two prisms made of different materials, it is possible to
(a) have dispersion without average deviation
(b) have deviation without dispersion
(c) have both dispersion and average deviation
(d) have neither dispersion nor average deviation
A certain material has refractive indices 1.56, 1.60 and 1.68 rfor red, yellow and violet lightespectively. (a) Calculate the dispersive power. (b) Find the angular dispersion produced by a thin prism of angle 6° made of this material.
A thin prism is made of a material having refractive indices 1.61 and 1.65 for red and violet light. The dispersive power of the material is 0.07. It is found that a beam of yellow light passing through the prism suffers a minimum deviation of 4.0° in favourable conditions. Calculate the angle of the prism.
Two prisms of identical geometrical shape are combined with their refracting angles oppositely directed. The materials of the prisms have refractive indices 1.52 and 1.62 for violet light. A violet ray is deviated by 1.0° when passes symmetrically through this combination. What is the angle of the prisms?
A thin prism of angle 6.0°, ω = 0.07 and μy = 1.50 is combined with another thin prism having ω = 0.08 and μy = 1.60. The combination produces no deviation in the mean ray. (a) Find the angle of the second prism. (b) Find the net angular dispersion produced by the combination when a beam of white light passes through it. (c) If the prisms are similarly directed, what will be the deviation in the mean ray? (d) Find the angular dispersion in the situation described in (c).
A ray of light is incident on a prism whose refractive index is 1.52 at an angle of 40°. If the angle of emergence is 60°, calculate the angle of the prism.
A narrow beam of monochromatic light, PQ, is incident normally on one face of an equiangular glass prism of refractive index 1.45. When the prism is immersed in a certain liquid, the ray makes a grazing emergence along the other face (See figure). Find the refractive index of this liquid. 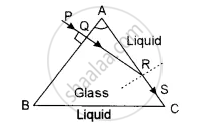
For any prism, obtain a relation between the angle of the prism (A), the angle of minimum deviation (δm) and the refractive index of its material (μ or n).
When a ray of white light is incident obliquely on the first surface of a prism, then ______.
