Advertisements
Advertisements
Question
For any prism, obtain a relation between the angle of the prism (A), the angle of minimum deviation (δm) and the refractive index of its material (μ or n).
Solution
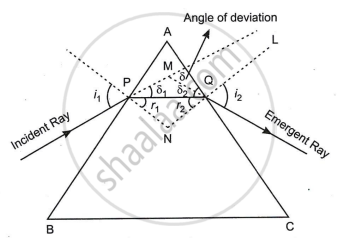
In the given diagram,
OP is the incident ray, which makes the angle i, with normal, and QR is the angle of emergence, which is represented by i2. A is the prism angle, and it is the refractive index of the prism.
Now, we know that,
A = Prism angle, δ = Angle of deviation
i1 = Angle of incidence
i2 = Angle of emergent
In the case of minimum deviation
∠r1 = ∠r2 = ∠r
A = ∠r1 + ∠r2 = ∠2r
`=> ∠"r" = "A"/2`
Now again
A + δ = i1 + i2 ...(∵ In the case of minimum deviation)
i1 = i2 = i and δ = δm
So, A + δm = i + i = 2i
Now, `angle "i" = ("A" + delta_"m")/2`
For Snell's law:
`mu = (sin i)/(sin r)`
`=> mu = (sin ("A" + delta_m)/2)/(sin "A"/2)`
APPEARS IN
RELATED QUESTIONS
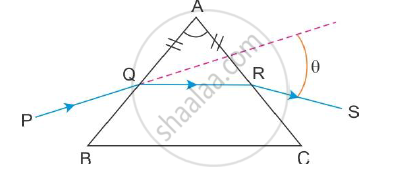
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60° and refractive index of material of prism is `sqrt3 `. Calculate angle θ.
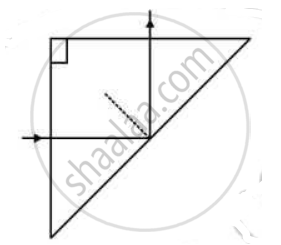
A ray of light incident normally on one face of a right isosceles prism is totally reflected, as shown in fig. What must be the minimum value of refractive index of glass? Give relevant calculations.
For any prism, prove that :
'n' or `mu = sin((A + delta_m)/2)/sin(A/2)`
where the terms have their usual meaning
The equation \[\omega = \frac{\mu_u - \mu_r}{\mu - 1}\] was derived for a prism having small refracting angle. Is it also valid for a prism of large refracting angle? Is it also valid for a glass slab or a glass sphere?
If three identical prisms are combined, is it possible to pass a beam that emerges undeviated? Undispersed?
If a glass prism is dipped in water, its dispersive power ___________ .
A prism can produce a minimum deviation δ in a light beam. If three such prisms are combined, the minimum deviation that can be produced in this beam is _______________.
A thin prism of angle 6.0°, ω = 0.07 and μy = 1.50 is combined with another thin prism having ω = 0.08 and μy = 1.60. The combination produces no deviation in the mean ray. (a) Find the angle of the second prism. (b) Find the net angular dispersion produced by the combination when a beam of white light passes through it. (c) If the prisms are similarly directed, what will be the deviation in the mean ray? (d) Find the angular dispersion in the situation described in (c).
How does the angle of minimum deviation of a glass prism vary if the incident violet light is replaced by red light?
When a ray of white light is incident obliquely on the first surface of a prism, then ______.
