Advertisements
Advertisements
Question
The vertices of the triangle are A(5, 4, 6), B(1, –1, 3) and C(4, 3, 2). The internal bisector of angle A meets BC at D. Find the coordinates of D and the length AD.
Solution
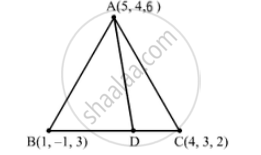
AB =\[\sqrt{4^2 + 5^2 + 3^2} = \sqrt{16 + 25 + 9} = \sqrt{50} = 5\sqrt{2}\]
\[\sqrt{1^2 + 1^2 + 4^2} = \sqrt{18} = 3\sqrt{2}\]
AD is the internal bisector of\[∠BAC\]
\[\therefore \frac{BD}{DC} = \frac{AB}{AC} = \frac{5}{3}\]
Thus, D divides BC internally in the ratio 5:3.
\[\therefore D \equiv \left( \frac{5 \times 4 + 3 \times 1}{5 + 3}, \frac{5 \times 3 + 3\left( - 1 \right)}{5 + 3}, \frac{5 \times 2 + 3 \times 3}{5 + 3} \right)\]
\[ \Rightarrow D \equiv \left( \frac{23}{8}, \frac{12}{8}, \frac{19}{8} \right)\]
\[ \Rightarrow D \equiv \left( \frac{23}{8}, \frac{3}{2}, \frac{19}{8} \right) \]
\[ \therefore AD = \sqrt{\left( 5 - \frac{23}{8} \right)^2 + \left( 4 - \frac{12}{8} \right)^2 + \left( 6 - \frac{19}{8} \right)^2}\]
\[ = \sqrt{\frac{{17}^2 + {20}^2 + {29}^2}{8^2}}\]
\[ = \sqrt{\frac{289 + 400 + 841}{8^2}}\]
\[ = \frac{\sqrt{1530}}{8}\]
APPEARS IN
RELATED QUESTIONS
A point C with z-coordinate 8 lies on the line segment joining the points A(2, –3, 4) and B(8, 0, 10). Find its coordinates.
Show that the three points A(2, 3, 4), B(–1, 2 – 3) and C(–4, 1, –10) are collinear and find the ratio in which C divides AB.
Find the ratio in which the line joining (2, 4, 5) and (3, 5, 4) is divided by the yz-plane.
Find the ratio in which the line segment joining the points (2, –1, 3) and (–1, 2, 1) is divided by the plane x + y + z = 5.
If the points A(3, 2, –4), B(9, 8, –10) and C(5, 4, –6) are collinear, find the ratio in which Cdivides AB.
If P(0, 1, 2), Q(4, –2, 1) and O(0, 0, 0) are three points, then ∠POQ =
If the extremities of the diagonal of a square are (1, –2, 3 and (2, –3, 5), then the length of the side is
The points (5, –4, 2), (4, –3, 1), (7, 6, 4) and (8, –7, 5) are the vertices of
In a three dimensional space the equation x2 – 5x + 6 = 0 represents
