Advertisements
Advertisements
Question
Two charges 2 μC and −2 µC are placed at points A and B 6 cm apart.
- Identify an equipotential surface of the system.
- What is the direction of the electric field at every point on this surface?
Solution
- The situation is represented in the given figure.

An equipotential surface is a plane on which total potential is zero everywhere. This plane is normal to line AB. The plane is located at the mid-point of line AB because the magnitude of charges is the same. - The direction of the electric field at every point on this surface is normal to the plane in the direction of AB.
APPEARS IN
RELATED QUESTIONS
Define an equipotential surface.
A regular hexagon of side 10 cm has a charge 5 µC at each of its vertices. Calculate the potential at the centre of the hexagon.
What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning?
(Hint: The earth has an electric field of about 100 Vm−1 at its surface in the downward direction, corresponding to a surface charge density = −10−9 C m−2. Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about + 1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)
Draw equipotential surfaces:
(1) in the case of a single point charge and
(2) in a constant electric field in Z-direction. Why are the equipotential surfaces about a single charge not equidistant?
(3) Can electric field exist tangential to an equipotential surface? Give reason
Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.
Why is there no work done in moving a charge from one point to another on an equipotential surface?
Draw the equipotential surfaces due to an electric dipole.
Depict the equipotential surface due to
(i) an electric dipole,
(ii) two identical positive charges separated by a distance.
Statement - 1: For practical purpose, the earth is used as a reference at zero potential in electrical circuits.
Statement - 2: The electrical potential of a sphere of radius R with charge Q uniformly distributed on the surface is given by `Q/(4piepsilon_0R)`.
Assertion: Electric field is discontinuous across the surface of a spherical charged shell.
Reason: Electric potential is continuous across the surface of a spherical charged shell.
Consider the following statements and select the correct statement(s).
- Electric field lines are always perpendicular to equipotential surface.
- No two equipotential surfaces can intersect each other.
- Electric field lines are in the direction of tangent to an equipotential surface.
Equipotentials at a great distance from a collection of charges whose total sum is not zero are approximately.
Equipotential surfaces are shown in figure. Then the electric field strength will be ______.
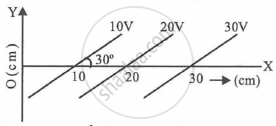
What is meant by an equipotential surface?
