Advertisements
Advertisements
Question
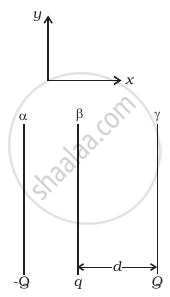
Two fixed, identical conducting plates (α and β), each of surface area S are charged to –Q and q, respectively, where Q > q > 0. A third identical plate (γ), free to move is located on the other side of the plate with charge q at a distance d (Figure). The third plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst β and γ.
- Find the electric field acting on the plate γ before collision.
- Find the charges on β and γ after the collision.
- Find the velocity of the plate γ after the collision and at a distance d from the plate β.
Solution
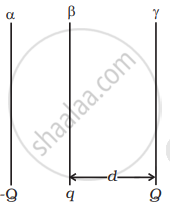
a. The electric field at γ due to plate α is `- Q/(S2ε_0) hatx`
The electric field at γ due to plate β is `q/(S2ε_0) hatx`
Hence, the net electric field is E1 = `((Q - q))/(2ε_0S) (- hatx)`
b. During the collision plates β and γ are together and hence must be at one potential. Suppose the charge on β is q1 and on γ is q2. Consider a point O. The electric field here must be zero.
Electric field at 0 due to α = `- Q/(2ε_0S) hatx`
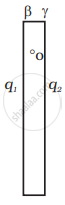
Electric field at 0 due to β = `q_1/(2ε_0S) hatx`
Electric field at 0 due to γ = `q_2/(2ε_0S) hatx`
∴ `(-(Q + q_2))/(2ε_0S) q_1/(2ε_0S)` = 0
⇒ q1 – q2 = Q
Further, q1 + q2 = Q + q
⇒ q1 = Q + q/2
And q2 = q/2
Thus the charge on β and γ are Q + q/2 and q/2, respectively.
c. Let the velocity be v at the distance d after the collision. If m is the mass of the plate γ, then the gain in K.E. over the round trip must be equal to the work done by the electric field. After the collision, the electric field at γ is
E2 = `- Q/(2ε_0S) hatx + ((Q + q/2))/(2ε_0S) hatx = (q/2)/(2ε_0S) hatx`
The work is done when the plate γ is released till the collision is F1d where F1 is the force on plate γ. The work done after the collision till it reaches d is F2d where F2 is the force on plate γ.
F1 = `E_1Q = ((Q - q)Q)/(2ε_0S)`
And F2 = `E_2 q/2 = (q/2)^2/(2ε_0S)`
∴ Total work done is `1/(2ε_0S) [(Q - q) Q + (q/2)^2]d = 1/(2ε_0S) (Q - q/2)^2d`
⇒ `(1/2)mv^2 = d/(2ε_0S) (Q - q/2)^2`
∴ `v = (Q - q/2)(d/(mε_0S))^(1/2)`
APPEARS IN
RELATED QUESTIONS
Explain the meaning of the statement ‘electric charge of a body is quantised’.
When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
It is now believed that protons and neutrons (which constitute nuclei of ordinary matter) are themselves built out of more elementary units called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so called ‘up’ quark (denoted by u) of charge (+2/3) e, and the ‘down’ quark (denoted by d) of charge (−1/3) e, together with electrons build up ordinary matter. (Quarks of other types have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.
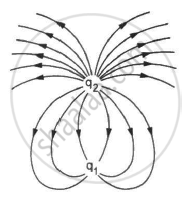
Consider the situation shown in the figure. What are the signs of q1 and q2? If the lines are drawn in proportion to the charges, what is the ratio q1/q2?
In Figure 1 below, a charge Q is fixed. Another charge q is moved along a circular arc MN of radius r around it, from the point M to the point N such that the length of the arc MN = l. The work done in this process is:
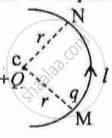
figure 1
Choose the correct option.
Two-point charges of A = +5.0 μC and B = -5.0 μC are separated by 5.0 cm. A point charge C = 1.0 μC is placed at 3.0 cm away from the centre on the perpendicular bisector of the line joining the two point charges. The charge at C will experience a force directed towards
Answer the following question.
State the law of conservation of charge.
Eight dipoles of charge of magnitude ± e are placed inside a cube. The total electric flux coming out of the cube will be:-
A steady current of 8 mA flows through a wire. The number of electrons passing through a cross-section of the wire in 10 s is ______.
