Advertisements
Advertisements
Question
Two uniform solid spheres having unequal masses and unequal radii are released from rest from the same height on a rough incline. If the spheres roll without slipping, ___________ .
Options
the heavier sphere reaches the bottom first
the bigger sphere reaches the bottom first
the two spheres reach the bottom together
the information given is not sufficient to tell which sphere will reach the bottom first
Solution
the two spheres reach the bottom together
Acceleration of a sphere on the incline plane is given by
\[a = \frac{g\sin\theta}{1 + \frac{I_{COM}}{m r^2}}\]
\[ I_{COM}\] for a solid sphere \[= \frac{2}{5}m r^2 \]
\[So, a = \frac{g\sin\theta}{1 + \frac{2m r^2}{5m r^2}} = \frac{5}{7}g\sin\theta\]
a is independent of mass and radii; therefore, the two spheres reach the bottom together.
APPEARS IN
RELATED QUESTIONS
Derive an expression for kinetic energy, when a rigid body is rolling on a horizontal surface without slipping. Hence find kinetic energy for a solid sphere.
Read each statement below carefully, and state, with reasons, if it is true or false;
The instantaneous speed of the point of contact during rolling is zero.
Read each statement below carefully, and state, with reasons, if it is true or false;
A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion
A solid sphere of mass 1 kg rolls on a table with linear speed 2 m/s, find its total kinetic energy.
A sphere cannot roll on
The following figure shows a smooth inclined plane fixed in a car accelerating on a horizontal road. The angle of incline θ is related to the acceleration a of the car as a = g tanθ. If the sphere is set in pure rolling on the incline, _____________.
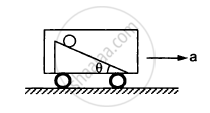
Answer in Brief:
A rigid object is rolling down an inclined plane derive the expression for the acceleration along the track and the speed after falling through a certain vertical distance.
A disc of the moment of inertia Ia is rotating in a horizontal plane about its symmetry axis with a constant angular speed ω. Another disc initially at rest of moment of inertia Ib is dropped coaxially onto the rotating disc. Then, both the discs rotate with the same constant angular speed. The loss of kinetic energy due to friction in this process is, ______
The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is, ______
A solid sphere rolls down from top of inclined plane, 7m high, without slipping. Its linear speed at the foot of plane is ______. (g = 10 m/s2)
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with velocity of 10 emfs. The total kinetic energy of sphere is ______.
A ring and a disc roll on horizontal surface without slipping with same linear velocity. If both have same mass and total kinetic energy of the ring is 4 J then total kinetic energy of the disc is ______.
An object is rolling without slipping on a horizontal surface and its rotational kinetic energy is two-thirds of translational kinetic energy. The body is ______.
A solid spherical ball rolls on an inclined plane without slipping. The ratio of rotational energy and total energy is ______.
If x = at + bt2, where x is the distance travelled by the body in kilometers while t is the time in seconds, then the unit of b is ______.
A disc of mass 4 kg rolls on a horizontal surface. If its linear speed is 3 m/ s, what is its total kinetic energy?
