Advertisements
Advertisements
Question
Use the mirror equation to show that an object placed between f and 2f of a concave mirror forms an image beyond 2f.
Solution
\[\text { For a concave mirror, the focal length (f) is negative } . \]
\[ \therefore f < 0\]
\[\text { When the object is placed on the left side of the mirror, the object distance (u) is negative } . \]
\[ \therefore u < 0\]
\[\text { For image distance v, we can write the mirror formula as }: \]
\[\frac{1}{f} = \frac{1}{v} + \frac{1}{u}\]
\[\frac{1}{v} = \frac{1}{f} - \frac{1}{u} . . . . . (i) \]
\[\text { The object lies between f and 2f }\]
\[ \Rightarrow 2f < u < f ( \because \text { u and f are negative })\]
\[ \frac{1}{2f} > \frac{1}{u} > \frac{1}{f}\]
\[ - \frac{1}{2f} < - \frac{1}{u} < - \frac{1}{f}\]
\[\frac{1}{f} - \frac{1}{2f} < \frac{1}{f} - \frac{1}{u} < 0\]
\[\text { Using equation (i), we get }: \]
\[\frac{1}{2f} < \frac{1}{v} < 0\]
\[ \therefore \frac{1}{v}\text { is negative, i . e . , v is negative }\]
\[\frac{1}{2f} < \frac{1}{v}\]
\[ 2f > v\]
Therefore, the image lies beyond 2f.
\[ - v > - 2f\]
APPEARS IN
RELATED QUESTIONS
a) Give two reasons to explain why reflecting telescopes are preferred over refracting type.
Use the mirror equation to show that an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
Using mirror formula, explain why does a convex mirror always produce a virtual image.
An object is kept on the principal axis of a concave mirror of focal length 10 cm. at a distance of 15
cm from its pole. The image formed by the mirror is:
(a) Virtual and magnified
(b) Virtual and diminished
(c) Real and magnified
(d) Real and diminished
Define the term 'limit of resolution'?
Use the mirror equation to show a convex mirror always produces a virtual image independent of the location of the object ?
Can a plane mirror ever form a real image?
A light ray falling at an angle of 45° with the surface of a clean slab of ice of thickness 1.00 m is refracted into it at an angle of 30°. Calculate the time taken by the light rays to cross the slab. Speed of light in vacuum = 3 × 108 m s−1.
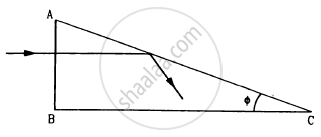
A light ray is incident normally on the face AB of a right-angled prism ABC (μ = 1.50) as shown in figure. What is the largest angle ϕ for which the light ray is totally reflected at the surface AC?
A point object is placed at a distance of 20 cm from a thin plano-convex lens of focal length 15 cm, if the plane surface is silvered. The image will form at: