Advertisements
Advertisements
Question
A light ray falling at an angle of 45° with the surface of a clean slab of ice of thickness 1.00 m is refracted into it at an angle of 30°. Calculate the time taken by the light rays to cross the slab. Speed of light in vacuum = 3 × 108 m s−1.
Solution
Given,
Angle of incidence, i = 45°
Angle of refraction, r = 30°
Using Snell's law,
\[\frac{\sin i}{\sin r} = \frac{3 \times {10}^8}{v}\]
\[= \frac{\sin 45^\circ}{\sin 30^\circ } = \frac{\left( \frac{1}{\sqrt{2}} \right)}{\left( \frac{1}{2} \right)}\]
\[= \frac{2}{\sqrt{2}} = \sqrt{2}\]
\[So, \]
\[ v = \frac{3 \times {10}^8}{\sqrt{2}} m/s\]
Let x be the distance travelled by light in the slab.
Now,
\[x = \frac{1 m}{\cos 30^\circ} = \frac{2}{\sqrt{3}} m\]
We know:
Time taken
\[= \frac{Distance}{Speed}\]
\[= \frac{2}{\sqrt{3}} \times \frac{\sqrt{2}}{3 \times {10}^8}\]
= 0.54 × 10−8
= 5.4 × 10−9 s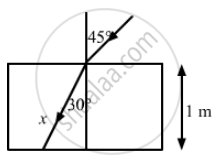
APPEARS IN
RELATED QUESTIONS
Use the mirror equation to show that an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
Use the mirror equation to deduce that an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
Using mirror formula, explain why does a convex mirror always produce a virtual image.
Define the term 'limit of resolution'?
A point source of light is placed in front of a plane mirror.
following Figure shows two rays A and B being reflected by a mirror and going as A' and B'. The mirror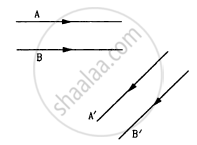
Which of the following (referred to a spherical mirror) do (does) not depend on whether the rays are paraxial or not?
(a) Pole
(b) Focus
(c) Radius of curvature
(d) Principal axis
Find the maximum angle of refraction when a light ray is refracted from glass (μ = 1.50) to air.
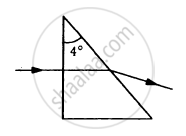
Find the angle of deviation suffered by the light ray shown in figure. The refractive index μ = 1.5 for the prism material.
Write any one use for each of the following mirrors :
(a) Convex
(b) Concave
Name the physical principle on which the working of optical fibers is based.
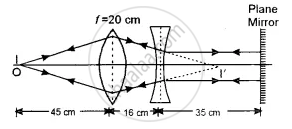
The figure below shows the positions of a point object O, two lenses, a plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.
For paraxial rays, show that the focal length of a spherical mirror is one-half of its radius of curvature.
A parallel beam of light is allowed to fall on a transparent spherical globe of diameter 30cm and refractive index 1.5. The distance from the centre of the globe at which the beam of light can converge is ______ mm.
When a clock is viewed in a mirror, the needles exhibit a time which appears to be 8:20. Then the actual time will be:
An upright object is placed at a distance of 40 cm in front of a convergent lens of a focal length of 20 cm. A convergent mirror of focal length 10 cm is placed at a distance of 60 cm on the other side of the lens. The position and size of the final image will be ______.
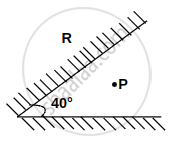
Two plane mirrors are inclined at an angle of 40°. The possible number of images of an object placed at point P would be?