Advertisements
Advertisements
Question
A converging mirror M1, a point source S and a diverging mirror M2 are arranged as shown in figure. The source is placed at a distance of 30 cm from M1. The focal length of each of the mirrors is 20 cm. Consider only the images formed by a maximum of two reflections. It is found that one image is formed on the source itself. (a) Find the distance between the two mirrors. (b) Find the location of the image formed by the single reflection from M2.
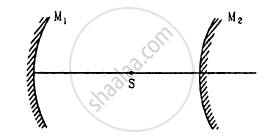
Solution
Given,
Converging mirror M1 with focal length (f1) = 20 cm
Converging mirror M2 with focal length (f2) = 20 cm
f1 = f2 = 20 cm = f
Point source is at a distance of 30 cm from M1.
As the 1st reflection is through the mirror M1,
u = −30 cm
f = −20 cm
Using mirror equation:
\[\Rightarrow \frac{1}{v} + \frac{1}{u} = \frac{1}{f}\]
\[\Rightarrow \frac{1}{v} + \frac{1}{- 30} = - \frac{1}{20}\]
\[\Rightarrow \frac{1}{v} = - \frac{1}{20} + \frac{1}{30}\]
\[ \Rightarrow \frac{1}{v} = - \frac{1}{60}\]
\[ \Rightarrow v = - 60 \text{ cm }\]
and for the 2nd reflection at mirror M2,
u = 60 − (30 + x) = 30 − x
v = − x, f = 20 cm
Again using the mirror equation:
\[\Rightarrow \frac{1}{30 - x} - \frac{1}{x} = \frac{1}{20}\]
\[\Rightarrow \frac{x - 30 + x}{x(30 - x)} = \frac{1}{20}\]
⇒ 40x − 600 = 30x − x2
⇒ x2 + 10x − 600 = 0
\[\Rightarrow x = \frac{10 + 50}{2} = \frac{40}{2}\]
= 20 cm or − 30 cm
∴ Total distance between the two lines is 20 + 30 = 50 cm
(b) Location of the image formed by the single reflection from M2 = 60 \[-\] 50 = 10
Thus, the image formed by the single reflection from M2 is at a distance of 10 cm from mirror M2.
APPEARS IN
RELATED QUESTIONS
Why can’t we see clearly through fog?
Show with the help of a diagram, how unpolarised light from Sun gets linearly polarised by scattering.
Describe briefly using a diagram how sunlight is polarised ?
A thin lens is made with a material having refractive index
\[\mu = 1 \cdot 5\]. Both the side are convex. It is dipped in water \[\mu = 1 \cdot 33\]. It will behave like
A point object O is placed on the principal axis of a convex lens of focal length f = 20 cm at a distance of 40 cm to the left of it. The diameter of the lens is 10 cm. An eye is placed 60 cm to right of the lens and a distance h below the principal axis. The maximum value of h to see the image is
A point source S is placed midway between two converging mirrors having equal focal length f as shown in figure. Find the values of d for which only one image is formed.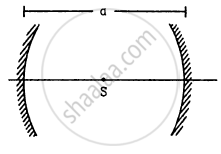
Locate the image of the point P as seen by the eye in the figure.

An optical fibre (μ = 1.72) is surrounded by a glass coating (μ = 1.50). Find the critical angle for total internal reflection at the fibre-glass interface.
A point source is placed at a depth h below the surface of water (refractive index = μ). (a) Show that light escapes through a circular area on the water surface with its centre directly above the point source. (b) Find the angle subtended by a radius of the area on the source.
A container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water = 4/3.
One end of a cylindrical glass rod (μ = 1.5) of radius 1.0 cm is rounded in the shape of a hemisphere. The rod is immersed in water (μ = 4/3) and an object is placed in the water along the axis of the rod at a distance of 8.0 cm from the rounded edge. Locate the image of the object.
Explain: ‘How is a rainbow formed’?
Answer the following question in detail.
Explain the formation of a primary rainbow. For which angular range with the horizontal is it visible?
Answer the following question in detail.
Explain the formation of a secondary rainbow. For which angular range with the horizontal is it visible?
Pick the wrong answer in the context with rainbow.
| Case study: Mirage in deserts |
 |
|
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts. Based on the above facts, answer the following question : |
In an optical fibre, if n1 and n2 are the refractive indices of the core and cladding, then which among the following, would be a correct equation?
| Case study: Mirage in deserts |
 |
|
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts. Based on the above facts, answer the following question: |
A diamond is immersed in such a liquid which has its refractive index with respect to air as greater than the refractive index of water with respect to air. Then the critical angle of diamond-liquid interface as compared to critical angle of diamond-water interface will
A short pulse of white light is incident from air to a glass slab at normal incidence. After travelling through the slab, the first colour to emerge is ______.
Between the primary and secondary rainbows, there is a dark band known as Alexandar’s dark band. This is because ______.
- light scattered into this region interfere destructively.
- there is no light scattered into this region.
- light is absorbed in this region.
- angle made at the eye by the scattered rays with respect to the incident light of the sun lies between approximately 42° and 50°.
