Advertisements
Advertisements
Question
Using Bohr’s postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transition between energy levels.
Advertisements
Solution
According to Bohr’s postulates, in a hydrogen atom, a single alectron revolves around a nucleus of charge +e. For an electron moving with a uniform speed in a circular orbit os a given radius, the centripetal force is provided by Columb force of attraction between the electron and the nucleus. The gravitational attraction may be neglected as the mass of electron and proton is very small.
So,
`(mv^2)/r = (ke^2)/r^2`
or `mv^2 = (ke^2)/r .............. (1)`
where m = mass of electron
r = radius of electronic orbit
v = velocity of electron.
Again,
`mvr = (nh)/(2π)`
or `v = (nh)/(2πmr)`
From eq.(1), we get,
`m((nh)/(2πmr)^2) = (ke^2)/r`
`=> r = (n^2h^2)/(4π^2kme^2).....................(2)`
(i) Kinetic energy of electron,
`E_k = 1/2 mv^2 = (ke^2)/(2r)`
Using eq (2), we get
`Ek =ke^2/2 (4π^2kme^2)/(n^2h^2)`
=`(4π^2kme^2)/(n^2h^2)`
`(2π^2k^2me^4)/(n^2h^2)`
(ii) Potential energy
`E_p = -(k(e) xx (e))/r = - (ke^2) / r `
Using eq (2), we get
`E^p =-ke^2 xx (4π^2kme^2)/(n^2h^2)`
= `-(4π^2k^2me^4)/(n^2h^2)`
Hence, total energy of the electron in the nth orbit
`E =E_p+E_k =(4π^2k^2me^4)/(n^2h^2)+(2π^2k^2me^4)/(n^2h^2) =- (2π^2k^2me^4)/(n^2h^2) =- (13.6)/n^2 eV `
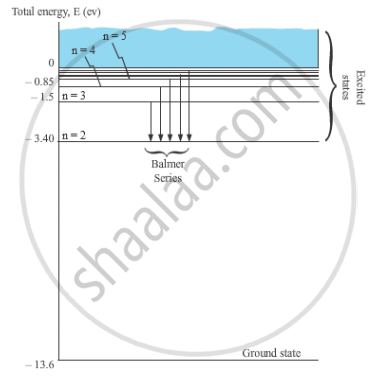
When the electron in a hydrogen atom jumps from higher energy level to the lower energy level, the difference of energies of the two energy levels is emitted as a radiation of particular wavelength. It is called a spectral line.
In H-atom, when an electron jumps from the orbit ni to orbit nf, the wavelength of the emitted radiation is given by,
`1/λ = R (1/n_f^2 -1/n_i^2)`
Where,
R → Rydberg’s constant = 1.09678 ×107 m−1
For Balmer series, nf = 2 and ni = 3, 4, 5, …
`1/λ = R (1/2^2 -1/n_i^2)`
Where, ni = 3, 4, 5, …
These spectral lines lie in the visible region.
APPEARS IN
RELATED QUESTIONS
Draw a neat, labelled energy level diagram for H atom showing the transitions. Explain the series of spectral lines for H atom, whose fixed inner orbit numbers are 3 and 4 respectively.
The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.
A neutron moving with a speed υ strikes a hydrogen atom in ground state moving towards it with the same speed. Find the minimum speed of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron = mass of hydrogen = 1.67 × 10−27 kg.v
Which of these statements correctly describe the atomic model according to classical electromagnetic theory?
Why was a change in the Bohr Model of atom required? Due to which important development (s), concept of movement of an electron in an orbit was replaced by, the concept of probability of finding electron in an orbital? What is the name given to the changed model of atom?
If a proton had a radius R and the charge was uniformly distributed, calculate using Bohr theory, the ground state energy of a H-atom when (i) R = 0.1 Å, and (ii) R = 10 Å.
The number of times larger the spacing between the energy levels with n = 3 and n = 8 spacing between the energy level with n = 8 and n = 9 for the hydrogen atom is ______.
In Bohr's atomic model of hydrogen, let K. P and E are the kinetic energy, potential energy and total energy of the electron respectively. Choose the correct option when the electron undergoes transitions to a higher level:
A 100 eV electron collides with a stationary helium ion (He+) in its ground state and exits to a higher level. After the collision, He+ ions emit two photons in succession with wavelengths 1085 Å and 304 Å. The energy of the electron after the collision will be ______ eV.
Given h = 6.63 × 10-34 Js.
State the Bohr's postulate of angular momentum of an electron.
