Advertisements
Advertisements
प्रश्न
Using Bohr’s postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transition between energy levels.
उत्तर
According to Bohr’s postulates, in a hydrogen atom, a single alectron revolves around a nucleus of charge +e. For an electron moving with a uniform speed in a circular orbit os a given radius, the centripetal force is provided by Columb force of attraction between the electron and the nucleus. The gravitational attraction may be neglected as the mass of electron and proton is very small.
So,
`(mv^2)/r = (ke^2)/r^2`
or `mv^2 = (ke^2)/r .............. (1)`
where m = mass of electron
r = radius of electronic orbit
v = velocity of electron.
Again,
`mvr = (nh)/(2π)`
or `v = (nh)/(2πmr)`
From eq.(1), we get,
`m((nh)/(2πmr)^2) = (ke^2)/r`
`=> r = (n^2h^2)/(4π^2kme^2).....................(2)`
(i) Kinetic energy of electron,
`E_k = 1/2 mv^2 = (ke^2)/(2r)`
Using eq (2), we get
`Ek =ke^2/2 (4π^2kme^2)/(n^2h^2)`
=`(4π^2kme^2)/(n^2h^2)`
`(2π^2k^2me^4)/(n^2h^2)`
(ii) Potential energy
`E_p = -(k(e) xx (e))/r = - (ke^2) / r `
Using eq (2), we get
`E^p =-ke^2 xx (4π^2kme^2)/(n^2h^2)`
= `-(4π^2k^2me^4)/(n^2h^2)`
Hence, total energy of the electron in the nth orbit
`E =E_p+E_k =(4π^2k^2me^4)/(n^2h^2)+(2π^2k^2me^4)/(n^2h^2) =- (2π^2k^2me^4)/(n^2h^2) =- (13.6)/n^2 eV `
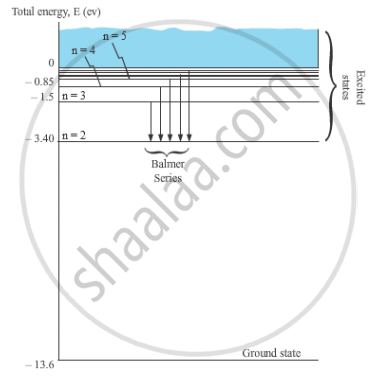
When the electron in a hydrogen atom jumps from higher energy level to the lower energy level, the difference of energies of the two energy levels is emitted as a radiation of particular wavelength. It is called a spectral line.
In H-atom, when an electron jumps from the orbit ni to orbit nf, the wavelength of the emitted radiation is given by,
`1/λ = R (1/n_f^2 -1/n_i^2)`
Where,
R → Rydberg’s constant = 1.09678 ×107 m−1
For Balmer series, nf = 2 and ni = 3, 4, 5, …
`1/λ = R (1/2^2 -1/n_i^2)`
Where, ni = 3, 4, 5, …
These spectral lines lie in the visible region.
APPEARS IN
संबंधित प्रश्न
Calculate the energy required for the process
\[\ce{He^+_{(g)} -> He^{2+}_{(g)} + e^-}\]
The ionization energy for the H atom in the ground state is 2.18 ×10–18 J atom–1
Suppose, the electron in a hydrogen atom makes transition from n = 3 to n = 2 in 10−8 s. The order of the torque acting on the electron in this period, using the relation between torque and angular momentum as discussed in the chapter on rotational mechanics is
A neutron moving with a speed υ strikes a hydrogen atom in ground state moving towards it with the same speed. Find the minimum speed of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron = mass of hydrogen = 1.67 × 10−27 kg.v
The spectral line obtained when an electron jumps from n = 5 to n = 2 level in hydrogen atom belongs to the ____________ series.
Why was a change in the Bohr Model of atom required? Due to which important development (s), concept of movement of an electron in an orbit was replaced by, the concept of probability of finding electron in an orbital? What is the name given to the changed model of atom?
The energy required to remove the electron from a singly ionized Helium atom is 2.2 times the energy required to remove an electron from Helium atom. The total energy required to ionize the Helium atom completely is ______.
The line at 434 nm in the Balmer series of the hydrogen spectrum corresponds to a transition of an electron from the nth to second Bohr orbit. The value of n is ______.
What is meant by ionisation energy?
The radius of the nth orbit in the Bohr model of hydrogen is proportional to ______.
The wavelength of the second line of the Balmer series in the hydrogen spectrum is 4861 Å. Calculate the wavelength of the first line of the same series.
